Если возникнет вопрос, откуда взялось

решение? как показать, или как описать так, чтобы этого вопроса не возникло.
Вы же своего решения не показали, поэтому конкретно указать место невозможно.
Я могу предположить, что Вы решали уравнение как однородное и использовали замену неизвестной функции вида

. В таком случае на одном из шагов решения возникло деление на

, которое возможно только при

, а Вы, таким образом, потеряли решения, для которых

. Это уравнение Вы должны были решить отдельно и получить функции

,

и

, которые следует подставить в уравнение и проверить, являются ли они решениями.

, естественно, решением не является, так как

— независимая переменная, но если бы уравнение было записано в виде
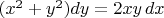
, то из него было бы не ясно, какая из переменных является независимой, и решения вида

были бы возможны.
Интегрируя уравнение для

, Вы могли получить что-нибудь вроде

Предвидя будущие преобразования, можно догадаться записать произвольную постоянную в виде

, где, разумеется,

, и после преобразований получается ваше общее решение (оно, кстати, никакое не "второе", а общее; у меня знак

получился противоположным вашему, но это не существенно и получилось в результате каких-то отличий в преобразованиях)

, где, как было сказано,

(нужно понимать, почему после раскрытия модулей можно не писать

). Если произвольную постоянную после интегрирования обозначить просто

, то, так как
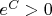
, убрав модули, придётся писать

.
Далее нужно вспомнить про три дополнительных решения и проверить, получаются ли они из общего при каком-нибудь значении

. При этом обнаруживается, что решения

и

получаются при

и, следовательно, требование

не нужно (а также в ответе не нужно указывать эти два решения отдельно от общего решения), а

ни при каком значении

не получается, и потому его в ответе нужно указать отдельно.
Единственность решения задачи Коши для данного уравнения нарушается только в точке

, поэтому особых решений нет; в частности, решение

является частным, а не особым.
Немного изменив вычисления, можно было бы получить общее решение в виде

, тогда

получалось бы при

, а решения

и

не получались бы ни при каком значении

.