Если я ошибаюсь, поправьте меня.
1.
"Определение 4.2 Мы говорим, что

есть билинейная функция (билинейная форма) от векторов

и
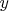
, если:
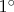
при фиксированном
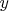

есть линейная функция от

,

при фиксированном


есть линейная функция от
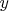
." (Гельфанд. Лекции по линейной алгебре, гл.1, §4, п.2.)
Чтобы понять, что это значит - при фиксированном

, - запишем билинейную функцию в виде произведения ее матрицы на координаты векторов по правилам перемножения матриц:

где элементы (одномерной) матрицы

фиксированы, поскольку фиксированы элементы матриц

и

.
Для фиксированного

можно провести аналогичную операцию.
2.
Билинейную форму можно получить, перемножив две линейные формы.
Положив

,

, перемножим две линейнные формы, а именно
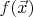
и

:

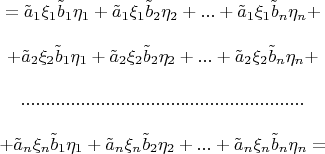

Положив

, получим


Если расположить эту сумму в виде матрицы - как она у нас и расположена, - можно представить ее как матрицу, все элементы которой складываются между собой. Такую матрицу можно назвать
аддитивной матрицей и обозначить
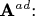

Из нее можно выделить матрицу

билинейной формы


Если умножить ее на координаты векторов

по правилу перемножения матриц (

слева,

справа), то получим аддитивную матрицу

:

Поскольку

, матрица

может быть представлена как матрица
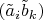
, причем матрица
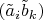
получается в результате тензорного перемножения матриц линейных функций (линейных форм)
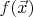
и

:
