Задачи из номера 19
"Математического Просвещения". См. также задачи из номеров
10,
11,
12,
13,
14,
15,
16,
17,
18.
1. В новогоднем конкурсе участвовало

человек. Все участники получили открытки. Занявшему первое место дали одну открытку и десятую часть оставшихся, за второе место дали две открытки и десятую часть оставшихся, ... за последнее

-е место —

открыток и десятую часть оставшихся. Все открытки были розданы. Сколько было участников?
(А. К. Ковальджи)2. В пространстве произвольным образом расположено несколько многогранников (возможно, пересекающихся). Докажите, что в пространстве можно расположить некоторое множество точек так, чтобы каждый многогранник содержал не менее одной точки внутри себя и чтобы любые два многогранника одинакового объёма содержали внутри себя одно и то же число точек.
(Г. А. Гальперин)3. Решите уравнения

в целых числах.
(Н. Н. Осипов)4. Расстояние между пунктами А и Б равно

. В пункте А имеется

велосипедистов и

велосипедов. Скорость пешехода

, велосипедиста

. За какое наименьшее время они могут добраться из пункта А в пункт Б? (Разрешается оставлять велосипеды на дороге.)
(А. Я. Канель-Белов) 5. Дана непрерывная поверхность без самопересечений. Известно, что на ней есть две точки, расстояние между которыми максимально для всех пар точек данной поверхности. Известно также, что любая её проекция есть круг. Докажите, что эта поверхность — сфера.
(А. А.Шапиро)6. Пусть

— иррациональное число,

— произвольное число из интервала

, а

— минимум дробной части

, где

— целое. Аналогично

есть минимум дробной части

. Докажите, что

при бесконечно многих

.
(Фольклор)7. Докажите неравенство

где

— радиусы описаннной и вписанной окружностей треугольника,
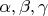
— его углы в радианах.
(К. Э. Каибханов)8. Многочлен

делит

при некотором

. Может ли один из его коэффициентов равняться

? А если

неприводим?
(В. А. Сендеров, А. Я. Канель-Белов)9. Дан треугольник

и положительные числа

такие, что

Пусть

— точка плоскости, для которой сумма

минимальна, а

— точки на сторонах

, для которых сумма

минимальна. Докажите, что

.
(А. А. Заславский)10. (Задача на исследование). На столе лежат круглые салфетки, возможно, разного размера. Любые две пересекаются. Докажите, что их можно прибить 100 гвоздями. Можно ли уменьшить число 100? А если эти салфетки суть единичные круги? А если это выпуклые фигуры, отличающиеся параллельным переносом?
(Фольклор)11. Плоскость раскрашена в несколько цветов. Докажите, что существует треугольник единичной площади с вершинами одного цвета.
(А. Я. Канель-Белов)12. При каких

существует такая бесконечная последовательность над алфавитом

, что никакая комбинация букв не повторится два раза подряд?
При каких

существует такая бесконечная последовательность над алфавитом

, что никакие три подслова одинаковой длины с одинаковой суммой символов не повторятся три раза подряд?
(Фольклор)Решения задач 3, 7, 9 приведены в
номере 20 (стр. 265-268)