Попробуем такой план. Поверим сказанному выше, что
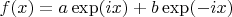
с некоторыми комплексными постоянными.
1. Тогда функция

удовлетворяет такой задаче Коши

Тогда

2. Предположим, что число

- действительное. Получаем

синус всё равно где-то обращается в единицу, поэтому для выполнения условия

нужно

.
3. Пусть теперь

- комплексное число. Действительная часть

,

и опять

.
Далее пока не получается. Может быть есть неединственность и все такие функции удовлетворяют условию задачи? Нужно требовать действительность функции с самого начала?