Вместо миноров можно инвариантно определяемые
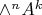
применить, где

, а

определяется на разложимых

-векторах как

Как частные случаи,

действует умножением на

, а

действует умножением на

. Остальные связаны с другими коэффициентами характеристического многочлена, там правда минусы где-то.
Если мы теперь посмотрим на
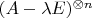
, оно биномиально превращается в сумму

, где остаётся только заметить, что
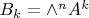
при подходящем определении

через

, и потому же

— умножающий на

оператор, а сумма, значит — умножающий на характеристический многочлен оператор. Конечно, теоремы о занулении этого многочлена на

это всё пока не даёт.
(А вот посмотрите какую ерунду я сочинил сейчас непонятно зачем)
Если теперь взять естественный изоморфизм

, действующий на разложимых тензорах

то посмотрим на

. С одной стороны если взять

,
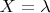
, тогда
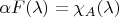
. С другой стороны в общем случае

разложится в сумму слагаемых

Введём теперь гомоморфизм
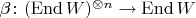
, просто перемножающий операторы в случае разложимого тензора:

. Если расширить

, чтобы он действовал «на левую половину»

, получим для каждого слагаемого

Наконец-то мы получили что-то многочленоподобное; правая часть действует умножением на скаляр, и её можно уже давно отождествить с соответствующим коэффициентом характеристического многочлена (и забыть про

), а левая это обычная степень оператора

. Ну ура, но откуда возьмётся факт, что вся сумма этих

равна нулю? Рассмотрим на

исходную функцию

. Её слагаемые
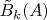
равны

и наверно уже очевидно, что я попытаюсь провернуть (и очевидно, что я где-то упустил минус). Подействуем ещё одним преобразованием

, перемножающим операторы в разложимых тензорных произведениях попарно, и получим

. Если бы минус был не забыт (я уже запутался, где; не стоило начинать этот велосипед), то

вышла бы равной

. Этого всё ещё мало, потому что это ещё не говорит, что и

(чтобы

как нам хочется). И вот тут честно говоря я сдаюсь. Мне даже уже кажется, что это просто переусложнённый вариант того самого неправильного доказательства с подстановкой матрицы перед вычислением определителя (по идее должен же был войти в игру присоединённый оператор, но где он?).
У кого-нибудь есть желание проверить?
UPD: Ага, мне в ЛС сказали, что действительно не работает. Ну что ж.