Наверно, не стоит слишком придираться к эмпирическим методам. А в силу нечёткости определения понятия "выброс" эмпирика здесь неизбежна.
По всей видимости, Тьюки выбирал коэффициент так, чтобы критерий был бы разумным для случая, когда измеряемая величина имела бы нормальное распределение. Но в случае ненормального был бы устойчив, что не выполняется для среднего, тем более для дисперсии, единичные большие выбросы их искажают драматически. Поэтому взяты квартили, не боящиеся 25% сколь угодно больших выбросов (а при везении даже при 50% работающие, если на каждый выброс в одну сторону приходится выброс в другую). Это снижение эффективности в сравнении с расчётом среднего и дисперсии, но не столь значительное, и заплатить этим за то, что выбросы не смогут замаскировать себя, завысив оценку разброса, стоит.
Квартиль нормального распределения отстоит от центра распределения на
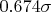
, то есть, если считать среднюю точку между квартилей оценкой центра распределения, критические точки будут отстоять от него на приблизительно

, и для нормального распределения вероятность превысить верхнюю точку составит около 0.005, а выйти за одну из границ около 1%. Более точные значения коэффициентов будут неудобны для расчётов (это работы достаточно давние, и предполагается, что расчёты делаются людьми, и как бы не в уме), а выигрыша в точности не дадут в силу нечёткости постановки зхадачи.