Тензор кручения в сферических координатах

[Alastoros]

При вычислении в МТУ символов Кристоффеля и тензора кривизны поверхности двумерной сферы, при дифференцировании множители Ламэ не используются, значит, при вычислении аффинной связности и далее тензора кривизны они используются не при дифференцировании, а только при преобразовании уже вычисленных тензоров к ортонормированным компонентам? А если вычислять неримановы величины, например тензор кручения, отождествляя антисимметричную часть метрического тензора с тензором электромагнитного поля, которое вычисляется в сферических координатах, при дифференцировании нормировочные множители не следует использовать? Но если при вычислении напряженности поля из потенциала в сферических координатах множители Ламэ используются, то перед вычислением тензора кручения сначала необходимо преобразовать их к неортонормированному виду?

[Утундрий]

Если имеется в виду нечто определённое (скажем, теория Ми), то об этом не худо бы сказать. Если же вопрос абстрактный, типа "Не ткнуть ли мне в глаз вилкой?", то ткните, может чего и вытечет (по меньшей мере глаз).

[Alastoros]

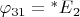
Например, есть элементарный диполь. Компоненты его поля ${E_1}$ и ${E_2}$. Кроме того, присутствует магнитное поле Земли, ${B_1}$ и ${B_2}$. Тогда компоненты антисимметричной части несимметричного метрического тензора по Эйнштейну должны быть ${{\varphi}_{23}} = {{{^*}E}_1}$, ${{\varphi}_{31}} = {{{^*}E}_2}$, ${{\varphi}_{01}} = {{{^*}B}_1}$, ${{\varphi}_{02}} = {{{^*}B}_1}$. Все отклонения симметричной части метрического тензора от галилеевых игнорировать. Аффинная связность может быть найдена по формуле Эйнштейна либо по формуле Дж. Томаса, в первом случае производные от антисимметричной части метрического тензора дадут тензор кручения, во втором - вклад в символы Кристоффеля. Тогда, чем именно являются эти компоненты антисимметричной части метрического тензора, что именно надо дифференцировать, чтобы найти этот тензор кручения? Допустим, что дифференцировать надо без использования множителей Ламэ, и только затем их использовать, если захочется привести найденные величины к ортонормированному виду. Но множители Ламэ использовались при нахождении ${E_1}$, ${E_2}$, ${B_1}$ и ${B_2}$, поэтому непонятно, можно ли написать ${{^*}E_1} = {E_1}$ и т.д., т.е. можно ли использовать напряженность электрического поля и индукцию магнитного поля напрямую, или сначала умножить на коэффициенты Ламэ, чтобы привести к неортонормированному виду? И если да, то какие именно, те, что использовались при нахождении компонент напряженности и индукции из потенциала (и тогда надо бы учитывать и фоновое электрическое поле Земли), т.е. ${1}$ для ${E_1}$ и ${B_1}$, и ${r}$ для ${E_2}$ и ${B_2}$, или по индексам тензора Эйнштейна, и тогда это будут множители ${1}$ для ${B_1}$, ${r}$ для ${B_2}$, ${{r^2}{\sin{\theta}}}$ для ${E_1}$ и ${{r}{\sin{\theta}}}$ для ${E_2}$?

[Утундрий]

Всё понятно, желаю всяческих успехов.

[Alex-Yu]

Похоже, кто-то развлекается с компьютерным бредогенератором "Корчеватель" номер 2. А в соседней ветке номер 3

Впрочем, учитывая успехи реформы образования, не исключено, что генератор не компьютерный, а биологический

[Утундрий]

Возможно, это такой тип "исследования" - надёргать отовсюду фактов, свалить в кучу и применить к ним случайную последовательность преобразований. В надежде, что из этой мешанины выползет что-то осмысленное.

[Pphantom]

Тема перемещена из форума «Помогите решить / разобраться (Ф)» в форум «Карантин»
по следующим причинам:

- пожалуй, это действительно надо бы привести к более осмысленному виду (в частности, пояснив, что и зачем делается).

Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.