Добрый день, глубокоуважаемые форумчане. У меня возник вопрос касательно того, что знает каждый младшекурсник, но в чем я, тем не менее, абсолютно запутался. Вопрос касается свойств симметрии векторов состояния систем тождественных фермионов. Постановки задачи могу выделить две, но они в целом эквивалентны друг другу с некоторыми оговорками.
1). Традиционная формулировка модели Изинга. Рассмотрим атомы, которые находятся в узлах пространственной решетки. Считаем, что внешние электроны слабо связаны с ядром и образуют некий "свободный газ", который нас не интересует. Делаем акцент на эффектах, связанных с внутренними электронами. Для простоты, пусть каждый атом имеет лишь один внутренний электрон в

-состоянии (т.е. без орбитального момента), тогда задача сводится к системе

спинов

.
2). Традиционная формулировка задач флюоресценции и сверхфлюоресценции. Пусть имеется

одноэлектронных атомов, которые находятся в резонаторе с частотой, резонансной с каким-либо атомным переходом. Тогда приближенно атомы можно рассматривать как двухуровневые системы (основное и возбужденное состояние), и задача сводится к системе

псевдоспинов

.
Если тензорно перемножать пространства

двухуровневых систем, то в полученном пространстве размерности

можно выделить подпространство максимального спина (псевдоспина)

. Базис этого подпространства называют состояниями Дике. Например, для трех частиц максимальный псевдоспин (в литературе иногда называют cooperation number) равен
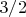
, и базис соответствующего подпространства образован состояниями Дике:

,

,

,

,
с проекциями спина (псевдоспина):

,

,

и
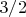
соответственно (прошу прощения, если пишу очевидные вещи). Как можно видеть, эти состояния симметричны относительно перестановки любых пар частиц, что справедливо и в общем для состояний

-частичного ансамбля

, где

. Поставленные задачи зачастую моделируются похожими Гамильтонианами, которые обладают такими же свойствами симметрии и в отсутствии взаимодействия диагональны в базисе Дике.
Что мне не ясно: общеизвестный и доказанный факт, что состояние системы тождественных частиц обладает определенными свойствами симметрии при перестановке пары частиц. Для бозонов --- симметричные, для фермионов --- антисимметричные. При этом, казалось бы, состояние Дике системы из

фермионов являются симметричными относительно любых перестановок частиц, независимо от того, является максимальный спин (псевдоспин)

целым или полуцелым. И никакой антисимметрии связанной с тем, что мы работаем с фермионами.
Какие были мысли:
1). ансамбль из

частиц типа ядро + фермион не эквивалентен ансамблю из

чистых фермионов. С другой стороны, принцип Паули безупречно работает при заполнении оболочек внутри каждого отдельного атома, а волновые функции многоэлектронных атомов строятся с опорой на теорему о связи спина со статистикой.
2). электроны в атомах не тождественны в том смысле, что каждый из них локализован около своего ядра, то есть не всегда можно ставить знак эквивалентности между неразличимыми частицами и состояниями, которые симметричны относительно перестановок частиц (возможно, сказал чушь). С другой стороны, в литературе рассматривают точечные системы (размер системы много меньше резонансной длины волны) и пренебрегают электростатическими межатомными взаимодействиями. В таких условиях нельзя сказать, что данный электрон локализован около определенного ядра, и электроны действительно неразличимы.
3). Вектор состояния симметричен, а вот волновую функцию нужно строить антисимметричной с учетом статистики. Но тогда состояния типа

не должны существовать, ведь все спины (псевдоспины) находятся в состоянии спин-вверх, и при построении волновой функции по определителю Слетера неизбежно будет ноль. Но это может значит, что детерминант Слетера -- очень грубое приближение, которое не учитывает перепутанность (невозможность тривиальной факторизации состояния на одночастичные) в такой многочастичной системе.
Тогда в чем дело, почему все-таки состояния системы
 фермионов проявляют бозонные свойства
фермионов проявляют бозонные свойства, и почему это не противоречит теореме о связи спина со статистикой? Как грамотно разрешить этот "парадокс"?
Очень прошу помочь мне разобраться в этом казалось бы "парадоксе", абсолютно уверен, что где-то сидит фундаментальное непонимание с моей стороны или пробел в знаниях. Спасибо!