Вариационная задача с ограничениями типа неравенств

[Red_Herring]

Давайте задачу 1.

Я понимаю, что в ограничении $\int_0^{\pi/2} f(x)=\mathsf{const}$ речь идет о конкретном значении (иначе никакого смысла нет). Т.е. мы хотим максимуизировать $I(f):=J^2(f)/2$ с ограничениями $K(f):=\int_0^{\pi/2} f\,dx=p $ , $1\ke f \le 1$ и $f(0)=1$, $f(\pi/2)=0$. Составляем

$$ I^*(f:)= I(f) -\lambda K(f)- \int_0^{\pi/2} \Bigl(\mu(x)f(x) +\nu(x)(1-f(x)) \Bigr)\,dx, $$

где $\lambda$, $\mu(x)$, $\nu(x)$ множители Л. , причем $\mu(x)\ge 0$, $f(x)>0\implies \mu(x)=0$ и $\nu(x)\ge 0$, $f(x)<1\implies \nu(x)=0$ в задаче максимизации (в задаче минимизации было бы $\mu(x)\le 0$ , ...

Это эквивалентно

$$ I^*(f:)= I(f) -\lambda K(f)- \int_0^{\pi/2} \omega(x) f(x)\,dx, $$

с $\omega:=\mu-\nu$, $0<f(x)<1\implies \omega(x)=0$, $f(x)=0\imlies \omega(x)\ge 0$, $f(x)=1\implies \omega(x)\le 0$.

Вариационное уравнение

$$ a \cos(x) + b\sin(x) -\lambda -\omega(x) =0,\qquad a = \int_0^{\pi/2}f(x)\cos(x)\,dx ,\ b=\int_0^{\pi/2}f(x)\sin(x)\,dx $$

или эквивалентно

$$\left\{ \begin{aligned} &a \cos(x) + b\sin(x) -\lambda =0 && 0<f<1,\\ &a \cos(x) + b\sin(x) -\lambda \ge 0 &&f=0,\\ &a \cos(x) + b\sin(x) -\lambda \le 0 &&f=1. \end{aligned}\right. $$

Из первого условия следует что $0<f<1$ ни на каком интервале быть не может, из второго и третьего, что $(0,\pi/2)$ разделен на два интервала, на одном $f=1$, на другом $f=0$. Остальное--сами

[DeBill]

George777
0. Совет Робертса, по большому счету, состоит в замене переменной $f$ на $g,$ такую, что для некоторой конкретной функции $\varphi$, принимающей значения из $[A,B]$ было $f=\varphi\circ g$. Не очень интересно, но возможно....

1. Вашу задачу, видимо, лучше всего рассматривать с точки зрения оптимального управления ($f$ - управление; ограничения на управление $0\leqslant f \leqslant 1$ задают выпуклое множество $U$ в $\mathbb{R}$, и т.д.).
2. Избавьтесь от корня (замените $J$ на $J_1=J^2$) . Растяжениями (заменой $f$ на $u=kf$) упростите ограничения. Составьте функцию Лагранжа
$L=J_1+\lambda (l(u)-1)$, где $l(u)=\int\limits_{0}^{\frac{\pi}{2}}u(t)dt$ .
Станет совсем хорошо: получится задача с квадратичным функционалом на выпуклом множестве (управлений со значениями в $U'=[0,C]$). Ну, и теперь учебники должны подсказать рецепт решения (теорема Куна-Такера? Выпуклый анализ?).
3. Граничные значения кажутся неестественными. Если искать решения в классе непрерывных ф-й (а Вы таки не написали об этом в постановке задачи), то таковых, видимо, и нет. А если без непрерывности - то гр. условия пропадают, и решений будет, видимо, куча.
4. Про конкретные Ваши задачи
1) Это задача переводится так: как распределить заданную массу (это - та Конст) по единичной окружности так, чтобы плотность везде была не боле единички, а центр масс был как можно дальше от начала координат? Ответ, вроде, очевиден...
2) Тот же вопрос, но для кривой на единичной сфере, заданной (в сферической сис. к-т) уравнением $\theta =\varphi (\varphi +a)$. Тут ответ не очевиден, и как раз мощная теория его (мобыть) и даст....

-- 14.05.2020, 15:27 --

Red_Herring в сообщении #1462642 писал(а):

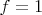
из второго и третьего, что $(0,\pi/2)$ разделен на два интервала, на одном $f=1$, на другом $f=0$.

Ага, вот и честное решение (Кун-Такер дадут ту же систему - эт те условия "дополняющей нежесткости"). Только одно дополнение: т.к. $a,b$ - неотрицательны, то система задает интервал, на котором функция равна 1 (вне него - а это может быть два интервала, примыкающие к концам - ф-я равна нулю).

[George777]

Прошу прощения за поздний ответ.

Red_Herring в сообщении #1462642 писал(а):

$$ I^*(f:)= I(f) -\lambda K(f)- \int_0^{\pi/2} \Bigl(\mu(x)f(x) +\nu(x)(1-f(x)) \Bigr)\,dx, $$

Это эквивалентно

$$ I^*(f:)= I(f) -\lambda K(f)- \int_0^{\pi/2} \omega(x) f(x)\,dx, $$

Скажите, а эквивалентость

$$ I^*(f:)= I(f) -\lambda K(f)- \int_0^{\pi/2} \Bigl(\mu(x)f(x) +\nu(x)(1-f(x))\Bigr)\,dx, $$

и

$$ I^*(f:)= I(f) -\lambda K(f)- \int_0^{\pi/2} \omega(x) f(x)\,dx, $$

рассматривается в плане одинаковости получающегося вариационного уравнения или чего? Просто в первом случае, как я понимаю, подынтегральное выражение с $\mu$ и $\nu$ тождественно равно нулю, в том числе и при $ f(x)=1$. А во втором случае при $ f(x)=1$ в подынтегральном выражении остается только $\omega$, которая в общем случае не равна нулю.
Я попробовал решить вторую задачу предложенным Вами методом, у меня получилась подобная Вашей система, первое уравнение

$$ a\cos(x)\sin(x(x+a)) + b\sin(x)\sin(x(x+a))+\cos(x(x+a)) -\lambda =0 , 0<f<1\\ $$

Из него так же следует, что промежуточных значений у $f$ нет. Получается, решение будет состоять из определенных последующими двумя уравнениями (приводить их не стал, они аналогичны Вашим) и нормировкой участков с 0 и 1.

DeBill в сообщении #1462660 писал(а):

Растяжениями (заменой $f$ на $u=kf$) упростите ограничения

Прошу не судить строго, я впервые в жизни слышу про оптимальное управление, Куна-Такера и выпуклый анализ. Что значит "упростить ограничения"? Разве $0\leqslant f \leqslant 1$ недостаточно просто? Как можно упростить?

DeBill в сообщении #1462660 писал(а):

А если без непрерывности - то гр. условия пропадают, и решений будет, видимо, куча.

Да, мне непрерывность не важна.

DeBill в сообщении #1462660 писал(а):

Тот же вопрос, но для кривой на единичной сфере, заданной (в сферической сис. к-т) уравнением $\theta =\varphi (\varphi +a)$. Тут ответ не очевиден, и как раз мощная теория его (мобыть) и даст....

Спасибо за геометрическую интерпретацию, очень наглядно. Для параметров моей задачи получается подобная кривулина.

DeBill в сообщении #1462660 писал(а):

Red_Herring в сообщении #1462642 писал(а):

из второго и третьего, что $(0,\pi/2)$ разделен на два интервала, на одном $f=1$, на другом $f=0$.

Ага, вот и честное решение (Кун-Такер дадут ту же систему - эт те условия "дополняющей нежесткости").

Вы про что-то такое имеете в виду?

[Red_Herring]

George777 в сообщении #1465339 писал(а):

Из него так же следует, что промежуточных значений у $f$ нет

В принципе, из нескольких участков, и надо проверять из скольки