Многозначная функция

[AKasyan]

В учебнике Л. Кудрявцева "Математический анализ" т.1, в разделе Определенный интеграл (обычный - Римана) вводится понятие предела многозначной функции (от разбиения) (см. с. 537). Само понятие многозначной функции не всеми авторами считается корректным. Если что-то устремляем, то какие значения куда-то стремятся? Но когда рассматриваются разбиения отрезка, то выхода нет, т.к. по условию разбиения произвольны. А функция от произвольных разбиений многозначна. Диаметр разбиения устремляют, как известно, к нулю, а множество сегментов, входящих в каждое разбиение, очевидно, устремляется в бесконечность, тем самым и функция стремится к бесонечнозначной. Может быть этот предельный переход является двойным? Как автор решает проблему? Почти дословно. Берем любую числовую последовательность рассматриваемых функций с конкретным разбиением и осуществляем предельный переход. Но по логике мы должны осуществлять предельный переход по множеству (т.е. перебирая все разбиения, другими словами, если так выразиться, по множеству всех произвольных разбиений, которое счетно). Это исходная точка сюжета, и одновременно устремляя диаметр к нулю (для решения задачи). Но чтобы не запутывать читателя, это все упрощают и говорят, что предельный переход осуществляем для любого разбиения и т.д. Кто нибудь рассматривал это вопрос более подробно. Например, можно рассмотреть такую функцию- модифицированную функцию Римана, для которой, как известно, существует интеграл (Римана). Изменим определение функции Римана, а именно, добавим следующее условие - в иррациональных алгебраических точках она равна единице (если нулю, то ничего не меняет (?)). Эта функция, наверное, уже не интегрируема по Риману. Но как доказывать, что в любом разбиении всегда встречается алгебраическое иррациональное число. Вот откуда и вопрос. Я не касаюсь проблемы упорядочения точек разбиения, так как множество действительных упорядочено, но каким способом? Это важно для нас.

[arseniiv]

Не помню чтобы там были многозначные функции, а уж тем более бесконечнозначные, можете ли вы привести цитату?

В обычном определении интеграла Римана не используется обычный предел, а берётся очень похожая конструкция, но подходящая к этой задаче. Говорится, что функция $f$ на отрезке $I$ интегрируема по Риману и имеет интеграл, равный $i$, если для любого $\varepsilon > 0$ существует $\delta > 0$ такое, что для любого разбиения $I$ на отрезочки длин меньше $\delta$ и любого выбора точек в них соответствующая интегральная сумма $s$ такова, что $|s-i|<\varepsilon$. Мне щас лень смотреть, что там в Кудрявцеве, но вот так и должно быть. Или там интеграл Дарбу, эквивалентный интегралу Римана.

Можно это определение сделать использующим предел, но сначала обобщить его и ввести дополнительную структуру на разбиениях. Опять же никакие многозначные функции не понадобятся.

[AKasyan]

arseniiv
По какому случаю упомянутое упорядочение (чисел, которые образуют разбиения) важно? Т.к. я выше привел модифицированную функцию Римана, то хотелось бы знать попало алгебраическое число в некоторый сегмент нашего (произвольного) разбиения или оно превышает границу сегмента и оказывается в другом (соседнем) сегменте. Как такие функции рассматривают (см. ф. Дирихле)? Смотрим на точки сегмента. Можно придумать функцию, которая зависит от этого. Размеры сегментов уменьшаются до нуля (но они не пусты - там, как минимум, одно число). Уменьшаем длину сегмента до нуля, но так, чтобы оставалось достаточно большое множество чисел, включая иррациональные. Но где окажутся упомянутые алгебраические? Алгебраические числа попадут в некоторые сегменты, т.к. их счетное множество, но это зависит от упорядочения. В некоторых может и не оказаться. Возвращаясь к исходному. Если мы берем какое-то разбиение, то почему отдельно рассматриваем числа, соответствующие этому разбиению? И разбиения и числа неразрывно связаны. Они прямо входят в формулу. Назовем такое разбиение обобщенным разбиением, включающим и сегменты разбиения и числа, которые выбираются произвольно на каждом сегменте. Такое множество должно иметь мощность выше континуума при неограниченном увеличении числа разбиений. Поэтому и функцию в пределе можно считать бесконечнозначной. Как ведут себя такие функции? Что на практике? На числовой оси отмечают точки и говорят, что это разбиение, а на каждом сегменте выбираем произвольную точку, делаем отметку. Вот и все доказательство. Более обстоятельно это рассматривается в интеграле Лебега. Поэтому могут сказать: зачем это все рассматривать, если по Лебегу все становится на свои места? Правильно, но только при условии, что интеграл по Риману всегда будет "дублироваться" интегралом по Лебегу. Но, как известно, для некоторых функций интеграл Римана существует, а Лебега нет. Поэтому относиться к интегралу Римана с пренебрежением не следует...
Цитата из Л.Кудрявцева (с. 537):"...Пусть на этом множестве определена числовая, вообще говоря, многозначная функция Ф(т), где т - разбиение отрезка...". Речь идет об определении, но которое смахивает на Теорему. В общем, с постановкой я совершенно согласен, т.к. по другому функцию, которая зависит от разбиения не назвать и она не однозначна (это какое-то отображение множества разбиений отрезка на числовую ось). В этом же определении уважаемого члена-корреспондента РАН рассматривается предел этой функции. Тут сложнее... Но интеграл Римана начинает приобретать несколько своеобразные очертания.

[Brukvalub]

AKasyan в сообщении #1459966 писал(а):

Уменьшаем длину сегмента до нуля, но так, чтобы оставалось достаточно большое множество чисел, включая иррациональные. Но где окажутся упомянутые алгебраические?

Я уверен, что не выпью столько, сколько нужно, чтобы начать это понимать!

[Otta]

AKasyan в сообщении #1459945 писал(а):

А функция от произвольных разбиений многозначна.

Почему?

[newUser23]

AKasyan в сообщении #1459945 писал(а):

Если что-то устремляем, то какие значения куда-то стремятся?

Вот Вы до сих пор встречались с вещественными функциями одного вещественного аргумента, т.е. с функциями вида $f: X \to \mathbb{R}, X \subset \mathbb{R}$. Понятие предела формулировалось именно для таких функций. Интегральная сумма - это тоже функция, но уже не такого вида. Она определена не на вещественных числах, а на множестве размеченных разбиений отрезка $[a, b]$. Интеграл Римана - это предел этой функции. Но Вам пока не говорили, что такое предел в таком, более общем случае. Самый простой выход из этой ситуации - прямо сформулировать определение интеграла Римана на языке $\varepsilon - \delta$ без произношения слова "предел". (хотя это конечно же и есть предел интегральных сумм по известной базе на множестве размеченных разбиений)

Цитата:

Говорят, что число $I$ является интегралом Римана от функции $f$ на отрезке $[a, b]$, если $\forall \varepsilon > 0 \exists \delta > 0$ такая, что для любого разбиения $(P, \xi)$ с отмеченными точками отрезка $[a, b]$, параметр которого $\lambda(P)<\delta$, имеет место соотношение

$$|I - \sum\limits_{i=1}^{n}f(\xi_i)\Delta x_i|<\varepsilon.$$

AKasyan в сообщении #1459945 писал(а):

А функция от произвольных разбиений многозначна.

Почему же? Интегральная сумма на вход берет некоторое размеченное разбиение отрезка $[a, b]$ а на выход выдает вещественное число - интегральную сумму, соответствующую этому разбиению.

AKasyan в сообщении #1459945 писал(а):

Например, можно рассмотреть такую функцию- модифицированную функцию Римана, для которой, как известно, существует интеграл (Римана). Изменим определение функции Римана, а именно, добавим следующее условие - в иррациональных алгебраических точках она равна единице (если нулю, то ничего не меняет (?)). Эта функция, наверное, уже не интегрируема по Риману.

Да, "если нулю", то Вы рассматриваете обычную функцию Римана. Ваша модифицированная функция будет разрывна в каждой иррациональной точке. Мерой множества иррациональных чисел на отрезке будет длина этого отрезка. Какой бы отрезок Вы бы ни Выбрали, множество точек разрыва Вашей функции на этом отрезке будет иметь ненулевую меру. Тогда согласно критерию Лебега интегрируемости функции, Ваша функция будет нигде не интегрируема по Риману.

-- 04.05.2020, 00:26 --

AKasyan в сообщении #1459966 писал(а):

Т.к. я выше привел модифицированную функцию Римана, то хотелось бы знать попало алгебраическое число в некоторый сегмент нашего (произвольного) разбиения или оно превышает границу сегмента и оказывается в другом (соседнем) сегменте. Как такие функции рассматривают (см. ф. Дирихле)?

Алгебраические числа всюду плотны среди вещественных. Какой бы маленький отрезок $[a, b] \subset \mathbb{R}$ вы бы ни выбрали, в нем будет бесконечно много алгебраических чисел. А по поводу функции Дирихле, там вообще все просто. Она же всюду разрывна. Поэтому она не интегрируема по Риману ни на каком отрезке.

AKasyan в сообщении #1459966 писал(а):

Размеры сегментов уменьшаются до нуля (но они не пусты - там, как минимум, одно число). Уменьшаем длину сегмента до нуля, но так, чтобы оставалось достаточно большое множество чисел, включая иррациональные. Но где окажутся упомянутые алгебраические? Алгебраические числа попадут в некоторые сегменты, т.к. их счетное множество, но это зависит от упорядочения. В некоторых может и не оказаться.

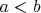
Говоря о сегменте $[a, b]$ обычно (хоть и не всегда) подразумевается, что $a < b$. При таком определении любой сегмент во-первых имеет ненулевую длину, во-вторых в этот сегмент попадут алгебраические числа, но не потому что их счетное множество, а потому что они всюду плотно располагаются на числовой оси.

AKasyan в сообщении #1459966 писал(а):

Но, как известно, для некоторых функций интеграл Римана существует, а Лебега нет. Поэтому относиться к интегралу Римана с пренебрежением не следует...

Это неправда. Если функция интегрируема по Риману на некотором отрезке, то она также интегрируема и по Лебегу на этом отрезке и оба интеграла равны.

[newUser23]

AKasyan в сообщении #1459966 писал(а):

Возвращаясь к исходному. Если мы берем какое-то разбиение, то почему отдельно рассматриваем числа, соответствующие этому разбиению?

Понятие разбиения $P$, размеченного разбиения $(P, \xi)$, набора точек $\xi = (\xi_1, ..., \xi_n), \xi_i \in [x_{i -1}, x_i]$ - это три разные вещи. Не путайте их.

AKasyan в сообщении #1459966 писал(а):

И разбиения и числа неразрывно связаны. Они прямо входят в формулу. Назовем такое разбиение обобщенным разбиением, включающим и сегменты разбиения и числа, которые выбираются произвольно на каждом сегменте.

Вы под "обобщенными разбиениями" видимо понимаете размеченные разбиения.

AKasyan в сообщении #1459966 писал(а):

На числовой оси отмечают точки и говорят, что это разбиение, а на каждом сегменте выбираем произвольную точку, делаем отметку. Вот и все доказательство.

Доказательство чего? Я в этом фрагменте вижу описание определения размеченного разбиения.

AKasyan в сообщении #1459966 писал(а):

Цитата из Л.Кудрявцева (с. 537):"...Пусть на этом множестве определена числовая, вообще говоря, многозначная функция Ф(т), где т - разбиение отрезка...". Речь идет об определении, но которое смахивает на Теорему.

Речь идет именно об определении, а не о теореме. $\Phi$(\tau)$ - да, многозначная функция. Кудрявцев ее вводит для того, чтобы сформулировать определение интеграла Римана на языке числовых последовательностей. Немного костыльно, но ничего страшного.

AKasyan в сообщении #1459966 писал(а):

В общем, с постановкой я совершенно согласен, т.к. по другому функцию, которая зависит от разбиения не назвать и она не однозначна (это какое-то отображение множества разбиений отрезка на числовую ось).

Вы же сами говорите, что функция не однозначная. Как она может тогда отображаться в числовую ось?

AKasyan в сообщении #1459966 писал(а):

В этом же определении уважаемого члена-корреспондента РАН рассматривается предел этой функции. Тут сложнее...

Возьмем произвольную последовательность разбиений $\tau_n$ стремящуюся к нулю. Если при произвольном выборе числа $\Phi_n(\tau_n)$ из значений $\Phi(\tau_n)$ последовательность $n \to \Phi_n(\tau_n)$ сходится к $A$, то $A$ - предел функции $\Phi$. Так понятнее?

[ewert]

newUser23 в сообщении #1459988 писал(а):

Речь идет именно об определении, а не о теореме. $\Phi$(\tau)$ - да, многозначная функция. Кудрявцев ее вводит для того, чтобы сформулировать определение интеграла Римана на языке числовых последовательностей. Немного костыльно, но ничего страшного.

Ничего страшного, если не считать полной бессмысленности этого определения. Поскольку у него не было определения даже многозначных функций, не говоря уж об их пределах.

А надо было и всего-то добавить к множеству всех разбиений множество наборов подчинённых им узлов -- и никакой многозначности. В общем, тут Кудрявцев сильно лажанулся.

Вот дальше, когда речь пойдёт о суммах Дарбу, подобного рода функция будет уже вполне уместной. Правда, называть её функцией всё же не очень хорошо. Главное, и необходимости-то никакой нет. Ведь не называл же он функцией свою $\sigma_{\tau}$. А она ничуть не менее функция, чем $\Phi(\tau)$; разве что (в отличие от $\Phi(\tau)$) корректна.

[ewert]

arseniiv в сообщении #1459950 писал(а):

функция $f$ на отрезке $I$ интегрируема по Риману и имеет интеграл, равный $i$, если для любого $\varepsilon > 0$ существует $\delta > 0$ такое, что для любого разбиения $I$ на отрезочки длин меньше $\delta$ и любого выбора точек в них соответствующая интегральная сумма $s$ такова, что $|s-i|<\varepsilon$. Мне щас лень смотреть, что там в Кудрявцеве, но вот так и должно быть.

У Кудрявцева, естественно, так и есть, только ещё грамотнее. Это -- определение "в стиле Коши", и Кудрявцев сразу же дублирует его определением "в стиле Гейне": число называется определённым интегралом, если к нему стремятся интегральные суммы для любой последовательности измельчающихся разбиений и наборов подчинённых им узлов.

Так что у Кудрявцева в этом месте всё было бы замечательно, не будь этой злосчастной $\Phi(\tau)$ (ну и ещё один дефект там есть, уже не слишком важный).

[newUser23]

ewert в сообщении #1460105 писал(а):

Поскольку у него не было определения даже многозначных функций, не говоря уж об их пределах.

Определение было.

Кудрявцев, стр. 21 писал(а):

Если $f:X \to Y$ и каждый элемент $y \in Y_f$ представляет собой множество каких-то элементов $y = \{z\}$, причем среди этих множеств $\{z\}$ имеется по крайней мере одно непустое множество, состоящее не из одного элемента, то такая функция $f$ называется многозначной функцией. При этом элементы $z$ множества $f(x) = \{z\}$ часто также называют значениями функции $f$ в точке $z$.

Вот это "имеется по крайней мере одно непустое множество, состоящее не из одного элемента" забавный оборот речи, но ладно. По поводу предела такой функции Кудрявцев говорит прямо: "Поэтому сформулируем общее определение предела этого вида". Кончено, как я уже говорил, это все костыли, но формально вроде все в порядке. Если уж и придираться, то придираться к самой природе многозначных функций. По крайней мере здесь можно было бы спокойно сказать, что элементами области значений той многозначной функции являются подмножества $\mathbb{R}$ и никаких многозначных функций не понадобилось бы.

ewert в сообщении #1460105 писал(а):

Вот дальше, когда речь пойдёт о суммах Дарбу, подобного рода функция будет уже вполне уместной.

А где там она нужны? Что суммы Дарбу, что интегралы Дарбу имеют исключительно прозрачные определения без всяких многозначных функций.

ewert в сообщении #1460105 писал(а):

Ведь не называл же он функцией свою $\sigma_{\tau}$.

Эта сигма-тау - как раз таки нормальная функция. Определена на размеченных разбиениях, принимает вещественные значения и называется интегральной суммой. Да, Кудрявцев не называет ее прямо функцией, но это вроде как должно быть очевидно.

ewert в сообщении #1460105 писал(а):

(в отличие от $\Phi(\tau)$) корректна.

$\Phi(\tau)$ вполне корректна, если считать ее значениями подмножества числовой прямой.

[ewert]

Ну хорошо. Пусть у него даже было формальное определение многозначной функции (практически бессмысленное, поскольку в той же ТФКП, скажем, где это определение легально -- оно и вполне конструктивно). Я ведь Кудрявцева не сканировал.

Но: где у него определение её предела?

По-моему, осмысленное определение предела функции, значениями которой являются множества, попросту невозможно.

Я уж не говорю о том, что понимается под предельной точкой. Ничего, разумеется.

[newUser23]

ewert в сообщении #1460315 писал(а):

Но: где у него определение её предела?

Кудрявцев, стр 537. писал(а):

Определение 3.Рассмотрим множество $\Gamma = \{\tau\}$ всех разбиений отрезка $[a, b]$. Пусть на этом множестве определена числовая, вообще говоря, многозначная функция $\Phi(\tau)$, $\tau \in \Gamma$. Будем говорить, что функция $\Phi(\tau)$ при $|\tau| \to 0$ имеет предел, равный $A$, и писать

$$\lim\limits_{|\tau| \to 0}^{}\Phi(\tau) = A,$$

если для любой последовательности разбиений $\tau_n \in \Gamma, n = 1, 2, 3...$, такой, что $\lim\limits_{n \to \infty}^{}|\tau_n| = 0$, при любом выборе значений $\Phi(\tau_n)$ числовая последовательность $\Phi(\tau_n)$ сходится к числу $A$, т.е.

$$\lim\limits_{n \to \infty}^{}\Phi(\tau_n) = A.$$

Это понятие предела определено с помощью понятия предела последовательности, поэтому для него справедливы многие свойства, аналогичные соответствующим свойствам предела последовательности.

Странное определение, согласен. По-моему Кудрявцев вводит эту конструкцию только лишь для того, чтобы иметь формальные основания называть интеграл пределом, но не вводить при этом базу.

ewert в сообщении #1460315 писал(а):

По-моему, осмысленное определение предела функции, значениями которой являются множества, попросту невозможно.

В общем случае возможно, если взять общетопологическое определение предела. Правда для этого область значений должна быть топологическим (а еще лучше хаусдорфовым) пространством.

[ewert]

newUser23 в сообщении #1460340 писал(а):

Правда для этого область значений должна быть топологическим (а еще лучше хаусдорфовым) пространством.

Это бессмысленно для элементарно высшего анализа.

newUser23 в сообщении #1460340 писал(а):

Странное определение, согласен. По-моему Кудрявцев вводит эту конструкцию только лишь для того, чтобы иметь формальные основания называть интеграл пределом, но не вводить при этом базу.

Ну т.е. Кудрявцев тут элементарно пижонит, притом на пустом месте. Ладно бы Зорич был какой. А у Кудрявцева оба исходных определения интеграла вполне корректны, и вполне дополняют друг друга.

Не понимаю, зачем ему понадобилось выёживаться. Выхлопа-то для дальнейшего всё равно нет.

-- Вт май 05, 2020 15:50:00 --

Да, по существу. В этом "определении" зависимость пресловутой Фи от узлов ни разу не упоминается. А ведь она есть -- иначе с какой бы стати обзывать эту Фи "многозначной" (пусть мы даже и не знаем, что под этим словом понимается). Соответственно, и "определение" лишено какого бы то ни было смысла.

-- Вт май 05, 2020 15:59:06 --

Могу, впрочем, предположить.
Когда это было -- в 80-м примерно году, кажется?
Ну так тогда идиотов было не меньше, чем сейчас.
Мол, давай в ногу. Выдавай фильтры с базами.
А то несовременненько выйдет.

Ну Кудрявцев -- человек слаб -- и поддался.

Это гипотеза.