Рассмотрим следующую конструкцию: Пусть

полукольцо подмножеств некоторого множества

и причем

может нe принадлежать

, т.е. возможно полукольцо без единицы. Пусть

-сигма-аддитивная мера на

и

где

. Заметим, что каждое

является полукольцом с единицей

. Ограничения

на

также является сигма-аддитивной мерой. Обозначим через

лебеговскую сигма-алгебру подмножеств

, полученную при продолжении меры

с полукольца

и

- соответствующую меру Лебега на

.
Определение: Пусть

. Тогда скажем

в том и только в том случае, когда для всякого

множество

. При этом если

то определим

Далее доказывается, что

является сигма-алгеброй и введенная на ней функция множества является сигма-аддитивной мерой.
Затем в книжке Ульянова-Дьяченко (да и в Колмогорова-Фомине) доказывается, что полученная сигма-алгебра

и мера

вовсе не зависят от способа представления множества

.
Ну пусть

и пусть

и

-сигма-алгебры и меры, соответствующие первому и второму разбиению, соответственно.
Как показать, что

и

. В этих книжках посмотрел но не разобрался никак.
Единственное что пока понял так это надо взять

. Я хочу проверить, что

, что равносильно

и

.
Возьмем

тогда по определению

для каждого

. Так как
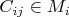
тогда

. Я знаю, что

. Как показать, что

? т.е.

для всякого

?