Задача:
Найти все пары

, при которых сходится интеграл

.
Пользуясь признаком Дирихле, я пришел к тому, что интеграл сходится при

, что совпадает с ответами. Но если в условиях признака Дирихле одна из функций не ограничена, то еще не факт, что исходный интеграл расходится. Например, при

несобственный интеграл

сходится на
![$(0,1]$ $(0,1]$](https://dxdy-01.korotkov.co.uk/f/0/f/c/0fc9b129aa8ad182cc2fc7bdd10830e782.png)
, причем
1) g(x) непрерывно дифференцируема на
![$(0,1]$ $(0,1]$](https://dxdy-01.korotkov.co.uk/f/0/f/c/0fc9b129aa8ad182cc2fc7bdd10830e782.png)
, правый предел в точке

равен

.
2) f(x) непрерывна на
![$(0,1]$ $(0,1]$](https://dxdy-01.korotkov.co.uk/f/0/f/c/0fc9b129aa8ad182cc2fc7bdd10830e782.png)
, и имеет НЕОГРАНИЧЕННУЮ первообразную на
![$(0,1]$ $(0,1]$](https://dxdy-01.korotkov.co.uk/f/0/f/c/0fc9b129aa8ad182cc2fc7bdd10830e782.png)
.
Поэтому в исходной задаче еще требуется доказать, что остальные пары

не подходят - при всех таких парах интеграл расходится.
Тут все мои идеи ограничиваются тем, чтобы, положив
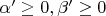
и предположив, что сходятся интегралы


прийти к противоречию.