Кубическая форма

[btoom]

Всем привет. Надо указать преобразование, переводящее
$C(x,y)=a x^3+b x^2 y+c x y^2+d y^3$
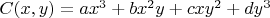
в
$C(\widetilde{x},\widetilde{y})=\widetilde{a} \widetilde{x}^3+\widetilde{c} \widetilde{x} \widetilde{y}^2$
или
$C(\widehat{x},\widehat{y})=\widehat{a} \widehat{x}^3+\widehat{d} \widehat{y}^3$
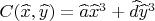
(это не существенно, какая форма).

Все коэффициенты вещественные, но неизвестен их знак. Преобразование, разумеется, должно быть обратимым. И при этом все входящие в формулы преобразования константы должны быть вещественными.

В этом и состоит загвоздка. Элементарными преобразованиями, указанными у Постона со Стюартом ("Теория катастроф и ее приложения"), все делается легко (все сводится к первой форме, но переход во вторую прост), только запросто так можно наткнуться на комплексные числа. Рассказываю, как.

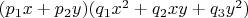
Суть подхода из книги: всякая кубическая форма представима произведением $(p_1 x+p_2 y)(q_1 x^2+q_2 xy+q_3 y^2)$. Очевидно, немедленно встает задача о разрешении переопределенной системы четырех квадратных уравнений:
$\begin{matrix} p_1 q_1=a,\\ p_1 q_2+p_2 q_1=b,\\ p_1 q_3+p_2 q_2=c,\\ p_2 q_3=d. \end{matrix}$

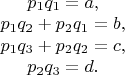
Задавая, к примеру, $q_1=1$, "новые" коэффициенты определяются очень просто через "старые". Причем делается это через решение кубического уравнения на один из "новых" коэффициентов.

Варианты для корней известны: три разных вещественных, один вещественный и два комплексно-сопряженных, два совпадающих и один отличный вещественный, три совпадающих вещественных. Короче говоря, хотя бы один вещественный да находится. И тогда "новые" коэффициенты вещественные.

Дальше надо описать квадратичную форму для $(q_1 x^2+q_2 xy+q_3 y^2)$. Это нужно для перехода к виду $(Lu+Mv)(u^2+v^2)$. Но нам не перейти к такому виду, не взяв квадратные корни из "новых" коэффициентов. Да, они обязательно будут вещественными, однако, знак их неизвестен.

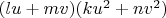
Тогда работаем с $(l u+m v)(k u^2+n v^2)$, но, увы, я никак не сумел перевести это дело к нужной форме. В книге указаны формулы лишь для единичных коэффициентов при квадратах. Я пытался делать преобразование Чирнгаузена как для u, так для v, но остаются "лишние" слагаемые. Сжатие, сдвиг, их комбинации, линейные замены - пока никак не помогло.

(Оффтоп)

В "Справочнике по теории плоских кривых третьего порядка" (Смогоржевский, Столова) сказано (глава 1, параграф 1, с.7), что Ньютон (Enumeratio linearum tertii ordinis) элементарными преобразованиями привел общее уравнение кривой третьего порядка к виду $xy^2+ey=ax^3+bx^2+cx+d$. Это идейно близко к тому, что мне надо, но в переводе, данном в сборнике "Ньютон. Математические работы" (советская книга 1937 года, пункт "Перечисление кривых третьего порядка") я не нашел его преобразований.

Я полагаю, что ответ где-то на поверхности. Буду признателен, если кто посоветует литературу или новый ход.

[nnosipov]

btoom в сообщении #1442860 писал(а):

Я полагаю, что ответ где-то на поверхности.

Правильно полагаете. Во-первых, заметьте, что можно считать $p_1=1$ и $p_2=0$ (иными словами, можно заменить $p_1x+p_2y$ на новое $x$). Во-вторых, выделите в квадратичной форме $q_1x^2+q_2xy+q_3y^2$ полный квадрат. Теперь после соответствующей линейной замены получится то, что надо.

[btoom]

nnosipov в сообщении #1442867 писал(а):

можно считать $p_1=1$ и $p_2=0$

Однако, если делать именно так, то незамедлительно следует, что $d=0$, что, вообще говоря, не так.

nnosipov в сообщении #1442867 писал(а):

иными словами, можно заменить $p_1x+p_2y$ на новое $x$

Пусть $p_1 x+p_2 y=\widetilde{x} \Rightarrow x=\frac{\widetilde{x}-p_2 y}{p_1}$.
Тогда имеем выражение
$\frac{\widetilde{x}}{p_1^2}(q_1 \widetilde{x}^2+\widetilde{x} y[q_2 p_1-2q_1 p_2]+y^2[q_1 p_2^2-q_2p_1p_2+q_3p_1^2])$.

Используем теперь преобразование Чирнгаузена $\widetilde{x}=X-\frac{\beta y}{3 \alpha}$, где греческими буквами обозначены постоянные, получаемые после раскрытия скобок - $\alpha $ это коэффициент при $\widetilde{x}^3$, $\beta y$ - то, что при $\widetilde{x}^2$.

В итоге получим $A X^3+BXy^2+Cy^3$, где большие латинские буквы это константы. И тут теперь надо исключить третье или второе слагаемое. Не готов навскидку сказать, как это сделать. Второй Чирнгаузен тут не поможет.

nnosipov в сообщении #1442867 писал(а):

Во-вторых, выделите в квадратичной форме $q_1x^2+q_2xy+q_3y^2$ полный квадрат. Теперь после соответствующей линейной замены получится то, что надо.

Для краткости переобозначив константы, получаем $\widetilde{x}(M[\widetilde{x}+\frac{N y}{2 M}]^2+y^2[K-\frac{N^2}{4M}])$. По-моему, на этом месте тупик. Даже если бы было нечто вроде $z(\lambda z - \mu t)^2=Z^2 (\frac{Z+ \mu t}{\lambda})|_{\lambda z - \mu t=Z}$, это все равно не то.

Возможно, не вполне корректно понял Вас. Уточните, пожалуйста.

[nnosipov]

btoom в сообщении #1443012 писал(а):

Для краткости переобозначив константы, получаем $\widetilde{x}(M[\widetilde{x}+\frac{N y}{2 M}]^2+y^2[K-\frac{N^2}{4M}])$. По-моему, на этом месте тупик.

Здесь полный квадрат нужно было по-другому выделить, т.е. привести к виду $\alpha x^2+\beta(\gamma_1x+\gamma_2y)^2$, после чего $\gamma_1x+\gamma_2y$ заменить на новый $y$.

[btoom]

nnosipov в сообщении #1443039 писал(а):

Здесь полный квадрат нужно было по-другому выделить, т.е. привести к виду $\alpha x^2+\beta(\gamma_1x+\gamma_2y)^2$, после чего $\gamma_1x+\gamma_2y$ заменить на новый $y$.

Понял теперь, спасибо. Короче говоря, алгоритм такой.
Форму

btoom в сообщении #1442860 писал(а):

$C(x,y)=a x^3+b x^2 y+c x y^2+d y^3$

сводим к

btoom в сообщении #1443012 писал(а):

$\frac{\widetilde{x}}{p_1^2}(q_1 \widetilde{x}^2+\widetilde{x} y[q_2 p_1-2q_1 p_2]+y^2[q_1 p_2^2-q_2p_1p_2+q_3p_1^2])$.

Чтобы довести слагаемые в скобке до формы

nnosipov в сообщении #1443039 писал(а):

$\alpha x^2+\beta(\gamma_1x+\gamma_2y)^2$

разрешаем переопределенную систему трех кубических уравнений на четыре новых коэффициента. Один из них делаем единицей и после легко определяются остальные (без всяких дополнительных уравнений). Заменяем эстетики ради $\widetilde{x}=X$ и еще

nnosipov в сообщении #1443039 писал(а):

$\gamma_1x+\gamma_2y$ заменить на новый $y$.

В итоге действительно останется $C_1 X^3+C_2 X Y^2.$. Еще раз благодарю.