Рассмотрим уравнение относительно


Здесь

суть некоторые параметры (на

дальше будут наложены дополнительные ограничения). Решение уравнения суть собственные числа оператора, порожденного некоторым уравнением с запаздыванием, но это здесь не существенно.
Требуется показать, что данное уравнение имеет ровно два простых корня (или возможно один корень кратности два) с

. В одной статье предлагается следующее рассуждение. Рассмотрим семейство уравнений при
![$\varepsilon \in [0,1]$ $\varepsilon \in [0,1]$](https://dxdy-02.korotkov.co.uk/f/9/a/8/9a8d92968607b7b1f931b9b47aaca39982.png)
:

Пусть

выбрано таким образом, что уравнения выше при любом
![$\varepsilon \in [0,1]$ $\varepsilon \in [0,1]$](https://dxdy-02.korotkov.co.uk/f/9/a/8/9a8d92968607b7b1f931b9b47aaca39982.png)
не имеют решений с

. Это равносильно неравенству

, где

таково, что
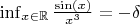
, что в принципе тоже не особо важно для моего вопроса. Легко видеть, что все уравнения имеют конечное число корней в любой полуплоскости

и они равномерно (по

) ограничены. Поэтому функция корней, лежащих в полуплоскости

, полунепрерывна сверху.
Далее - ключевой момент, который меня смущает. Поскольку корни непрерывно зависят от

и нет корней с

, то уравнение при

имеет в полуплоскости

столько же корней сколько их при

(а их, как легко видеть, - два простых).
Собственно смущает меня то, что из непрерывности корней не следует, что их не может появиться новых (и новые необязательно должны перейти через прямую

). Например, в семействе
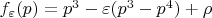
три корня при

и четыре корня при

(конечно здесь их сразу появляется четыре при любом

). То есть проблемы получаются при возмущении уравнения малой степени функцией большей степени, что как раз и происходит в исходных уравнениях. Можно ли подправить вышеприведенные рассуждения, чтобы доказать утверждение про корни?