Для простых

имеется элементарное решение (без гипотезы Римана).
Пусть

. Квадраты не представляются в таком виде только при

(

).
Если

, то

.
Ecли

не простое, то
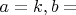
минимальный простой делитель

,

.
В противном случае

. Если

четное, то

.
Если

и

не делит

, то

. Пусть

. Возьмем в качестве

, если

четное, иначе

или

.
При этом

.
Следовательно, осталось рассмотреть только случай, когда

.
Если

, то

.
Остается только случай

.
Если

простое, то

, и

. При этом

. Такими являются только
