n l_min Δ
3 2 0
5 3 1
7 3 0
9 4 1
11...15 4 0
17 5 1, 2
19, 21 5 1
23...31 5 0
33, 35 6 2
37...41 6 1
43...63 6 0
65...73 7 2
75...85 7 1
87...127 7 0
129...145 8 2
147...169 8 1
171...185 8 0, 2, 3
187...203 8 0, 2
205...255 8 0
257...291 9 2
293...341 9 1
343...371 9 3
373...409 9 2
411...511 9 0
513...585 10 2
587...681 10 1
683...743 10 3
745...819 10 2
821...1023 10 0
1025...1169 11 2
1171...1365 11 1
1367...1489 11 3
1491...1637 11 2
1639...2047 11 0

 альтернатив?
альтернатив? - один раз бросаем монетку и безотносительно к результату выбираем первый вариант.
- один раз бросаем монетку и безотносительно к результату выбираем первый вариант. - один раз бросаем монетку и в случае выпадения "орла" выбираем первый вариант.
- один раз бросаем монетку и в случае выпадения "орла" выбираем первый вариант. - ...э-э-э...
- ...э-э-э... символов с вероятностью
символов с вероятностью  . Как с его помощью выбрать из трех вариантов?
. Как с его помощью выбрать из трех вариантов? - то мы уже точно в первой трети, дальше можно не бросать)?
- то мы уже точно в первой трети, дальше можно не бросать)?
 то в первом случае имеем среднюю длину
то в первом случае имеем среднюю длину  а во втором:
а во втором: 

 .
. бросков. Только последовательность всех единиц считаем ничейной. В противном случае возвращаем остаток от деления двоичного кода на
бросков. Только последовательность всех единиц считаем ничейной. В противном случае возвращаем остаток от деления двоичного кода на  .
. бросков для числа
бросков для числа  . В качестве ответа выдаём двоичный код, делённый на цело на
. В качестве ответа выдаём двоичный код, делённый на цело на  , если код не равен
, если код не равен  .
. броском даёт в среднем меньшее число бросаний.
броском даёт в среднем меньшее число бросаний. по сериям из трех бросков нам точно понадобится хотя бы одна серия, а с вероятностью
по сериям из трех бросков нам точно понадобится хотя бы одна серия, а с вероятностью  - хотя бы еще одна. Т.е. бросков в среднем уж точно не меньше чем
- хотя бы еще одна. Т.е. бросков в среднем уж точно не меньше чем  .
. , а нам в среднем нужно
, а нам в среднем нужно  серий до первой успешной, то
серий до первой успешной, то  , откуда
, откуда  (мат. ожидание геометрического распределения).
(мат. ожидание геометрического распределения).
 а для четырёх бросаний (
а для четырёх бросаний ( Для
Для  Выходит, более длинная серия всё-таки иногда бывает выгоднее.
Выходит, более длинная серия всё-таки иногда бывает выгоднее. минимальное число бросков в серии
минимальное число бросков в серии 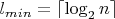 может оказаться неоптимальным. Надо брать различные
может оказаться неоптимальным. Надо брать различные  , для которых вероятность удачи в первой серии равна
, для которых вероятность удачи в первой серии равна  и смотреть чему равно среднее количество бросаний
и смотреть чему равно среднее количество бросаний 
 в знаменателе оптимальное
в знаменателе оптимальное  должно отличаться от
должно отличаться от  не на много.
не на много. и смотреть на то, как она меняется с ростом
и смотреть на то, как она меняется с ростом  для чисел близких, но меньших
для чисел близких, но меньших  . Неожиданно на мой взгляд то, что возможно несколько оптимальных значений. Или то, как дельта меняется при росте от
. Неожиданно на мой взгляд то, что возможно несколько оптимальных значений. Или то, как дельта меняется при росте от  : сначала 2, потом 1, затем 3, снова 2 и после этого 0. Я полагал, что будет что-нибудь типа 3, 2, 1, 0.
: сначала 2, потом 1, затем 3, снова 2 и после этого 0. Я полагал, что будет что-нибудь типа 3, 2, 1, 0. , где
, где  , где
, где  , и что-то оно как-то не похоже на
, и что-то оно как-то не похоже на  для не степеней 2 (ибо как минимум рационально). Хм.
для не степеней 2 (ибо как минимум рационально). Хм. и соответственно больше чем
и соответственно больше чем  отрезков мы. Если мы сделали
отрезков мы. Если мы сделали  бросков, то мера множества, в котором мы этого не знаем, максимум
бросков, то мера множества, в котором мы этого не знаем, максимум  , т.к.
, т.к.  отрезков, и "плохие" из них только те, в которые попала хотя бы одна из
отрезков, и "плохие" из них только те, в которые попала хотя бы одна из  границ. Соответственно с вероятностью экспоненциально быстро стремящейся к
границ. Соответственно с вероятностью экспоненциально быстро стремящейся к  при
при  мы сможем выдать
мы сможем выдать  раз - т.е. в среднем нам почти наверное понадобится как раз
раз - т.е. в среднем нам почти наверное понадобится как раз