Замечательно, конечно, что для двумерного случая так много сделано, но меня-то вообще говоря больше интересует случай общий:

на который вся эта изощрённая ТФКП вряд ли переносится. Буду пока что держать
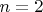
в уме и попытаюсь понять, что можно сделать для произвольного

. Локально, разумеется, локально.
Деривационных формулы для рассматриваемого случая имеют вид

Тогда метрика на поверхности есть

, а нормаль удовлетворяет естественным требованиям

и

Условия интегрируемости
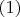
дают

А минимальность
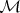
эквивалентна условию

Из
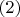
и
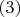
выводятся полезные соотношения

и

.
Теперь рассмотрим изогнутую поверхность

где

и найдём на ней метрику. Для этого вычислим новые касательные векторы

где введены следующие обозначения

Всюду ниже будем пренебрегать членами выше первого порядка малости по
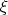
и
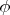
. Тогда метрика на

даётся выражением

Отсюда видно, что необходимым условием изометричности изгибания будет

, что приводится к виду

Из
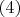
можно извлечь

, что можно переписать как

.
Мы хотим, чтобы изогнутая поверхность также была минимальна. Для формулировки соответствующего необходимого условия нам понадобятся коэффициенты возмущенной второй квадратичной формы

. Имея таковые, искомое условие запишем в виде

Общий вид возмущённой нормали

после удовлетворения условиям

конкретизируется до

Вычисление вторых производных возмущенного радиус-вектора приводит к

где

Условие минимальности принимает вид

или, после всех подстановок,

Что (внезапно!) оказывается возможным выразить в терминах одной только внутренней геометрии поверхности
