Вопрос распадается на два подвопроса: зачем вообще это в главе про перестановки, и как доказать данное утверждение.
Затем, что число перестановок факториал, и в большом числе практических задач (не только теорвера) достаточная точность достигается без перемножения n сомножителей, а по формуле Стирлинга, причём часто требуется отношение числа перестановок, и удаётся сократить числитель со знаменателем. То есть советуют необязательный, но весьма полезный инструмент.
А для доказательства надо знать о формуле Стирлинга чуть больше. А именно, что это

приближение, полученное из разложения факториала в ряд Стирлинга, в котором надо ещё домножить на
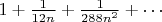
. Для строгого доказательства надо дать оценку отброшенным членам, но если ограничиться поправкой на

, получим вместо "просто-стирлинга", дающего

величину

, то, что и требовалось.
Ну, или можно взять оценку

где

, и тоже придти к оценке, которая заказана, взяв наихудшее значение для тэты.