Привет всем! Тема своеобразная, прошу не пинать сильно

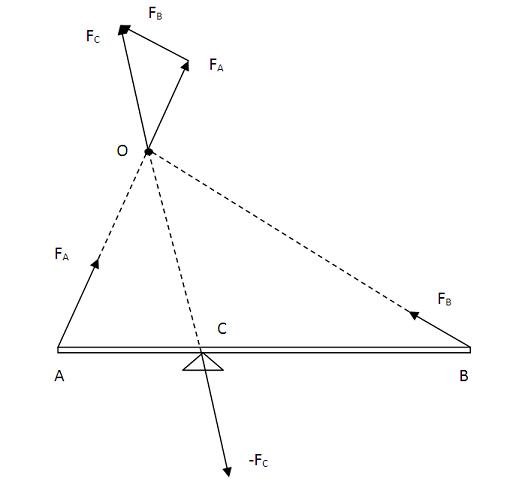
Закон рычага обычно выводится из закона сохранения энергии (см. напр. википедию). Но как-то однажды я нашел еще один вариант получения этого закона из других принципов, который хотелось бы обсудить. Ниже на рисунке показан рычаг, к концам которого приложены силы

и

, имеющие составляющие параллельно рычагу, причем сами силы не параллельны. Тогда есть точка

пересечения этих сил в пространстве. Если построить результирующую этих сил

, то ее продолжение пересечет точку опоры рычага

, в которой сила реакции опоры равна по модулю этой силе, но направлена в противоположную сторону для ее компенсации (система неподвижна). Таким образом, силы на концах рычагов и реакция опоры ведут себя так, как будто встретились в пространстве в точке

и скомпенсировали друг друга! Закон сохранения энергии в данном случае будет вытекать из этого положения... Какие мнения по этому результату?..