Написал пару последовательностей на PARI/GP, думаю, что они полны по критерию Брауна:
1)
![$a_1=[2, 1, 3, 5, 7, 17, 19, 50, 64, 152, 190, 470, 598, ....]$ $a_1=[2, 1, 3, 5, 7, 17, 19, 50, 64, 152, 190, 470, 598, ....]$](https://dxdy-04.korotkov.co.uk/f/f/f/1/ff1bcfef3040bdf69fd44c9a62b1e99582.png)

;

;


следующее число после

, которое не может быть представлено в виде

и
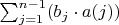
, где

,

(PARI)
Код:
{a=[1]; b=[]; for(i=1, 800, forsubset(#a, x, b=concat(b, [vecsum(vecextract(a, x))])); b=setminus(vecsort(b,,8),a); for(j=1, #a, b=concat(b, [2*a[j]]); b=vecsort(b,,8)); if(setsearch(b, i)==0, a=concat(a, [i]); a=vecsort(a,,8)) )}
Вторая последовательность строится также, только начальные значения другие:
![$a_2=[3, 1, 2, 5, 9, 13, 31, 35, 92, 118, 280, 350]$ $a_2=[3, 1, 2, 5, 9, 13, 31, 35, 92, 118, 280, 350]$](https://dxdy-04.korotkov.co.uk/f/7/8/f/78f0ea2ba411ad036a445f1bdef41aa382.png)
PARI
Код:
{a=[1, 2]; b=[]; for(i=1, 800, forsubset(#a, x, b=concat(b, [vecsum(vecextract(a, x))])); b=setminus(vecsort(b, , 8), a); for(j=1, #a, b=concat(b, [2*a[j]]); b=vecsort(b, , 8)); if(setsearch(b, i)==0, a=concat(a, [i]); a=vecsort(a, , 8)) ); print(a)}
upd:
Ещё одна последовательность:
![$a=[1, 2, 3, 7, 15, 29, 45, 101, 115, 302, 388, ....]$ $a=[1, 2, 3, 7, 15, 29, 45, 101, 115, 302, 388, ....]$](https://dxdy-04.korotkov.co.uk/f/f/7/2/f72ef7bd96216c313cb654a749c6fa9782.png)
Код:
{a=[1, 2, 3]; b=[]; for(i=1, 400, forsubset(#a, x, b=concat(b, [vecsum(vecextract(a, x))])); b=setminus(vecsort(b, , 8), a); for(j=1, #a, b=concat(b, [2*a[j]]); b=vecsort(b, , 8)); if(setsearch(b, i)==0, a=concat(a, [i]); a=vecsort(a, , 8)) ); print(a)}