Навеяно задачей
105176 с problems.ru.
Я прошу прощения за сумбур, но в силу отсутствия (?) практической ценности задачи сложно следить за строгостью всех формулировок.
Дело в том, что у этой задачи есть поразительная особенность... но о ней в самом конце.
Итак.
Рассмотрим приведенный квадратный трехчлен с целочисленными коэффициентами:

Приведем в соответствие ему набор трехчленов

и запишем последовательность их меньших корней:

(второй корень, конечно, равен

)
Будем называть трехчлен полностью целочисленным ранга

, если числа

- дробные (вообще говоря, иррациональные), а для всех

.
Собственно, теперь можно сформулировать задачу: для каких  трехчлен
трехчлен 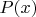 является полностью целочисленным ранга
является полностью целочисленным ранга  ?
?Ниже приводится простыня моего решения для некоторых случаев, поэтому дополнительные вопросы я приведу прямо сейчас:
1. Привести хотя бы один пример нетривиального решения для пятого ранга, или доказать, что решений не существует.
2. Формализовать общее решение для четвертого ранга.
------Трехчлен бесконечного ранга, как можно заметить, имеет вид

. Такое решение будем далее называть тривиальным.
А что для меньших рангов?
Далее для пущего удобства лучше говорить не о ранге

, а о ранге "по крайней мере,

", то есть не проверяем дробность

.
В принципе, любой полностью целочисленный трехчлен генерируется из своих корней, если они целые:

Но ранг его таким образом заранее нельзя предугадать.
Выпишем дискриминанты, которые, разумеется, для обеспечения целочисленности корней должны быть полными квадратами:

Обратим внимание, что

.
Итак, задача сводится к поиску таких

различных квадратов, что разности между каждой парой соседних по величине квадратов - прогрессия из нечетных чисел с шагом 2. Квадраты

последовательных чисел, как легко убедиться, удовлетворяют этому требованию и определяют тривиальное решение.
Вывод 1. Зная два дискриминанта и их порядковые номера, мы можем определить все остальные. ------
Пойдем по возрастанию сложности.
Второй ранг (напоминаю, что здесь это "по крайней мере, второй"): два квадрата с разностью

. То есть, мы можем взять любые два числа различной четности
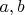
. Тогда определим

. Тогда

- имеет ранг не менее 2.
Вывод 2. Зная два первых дискриминанта, мы можем определить коэффициенты первого трехчлена.------
Для третьего ранга верно соотношение:

,
где
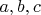
- целые (можно даже ограничиться неотрицательными), а их квадраты - необходимые нам дискриминанты

.
Чтобы решить его в целых числах, делаем подстановку

(

, как легко установить, нечетное), и приходим к выражению

Таким образом, поиск трехчленов третьего ранга может быть формализован следующим образом:
1) Задаемся нечетным

2) Рассматриваем разложение на два множителя величины

3) Тогда корни из дискриминантов равны:



4) Через
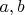
вычисляется

, а затем

.
5) Если поменять местами

и

, получится еще один трехчлен (проще: этому соотвутствуют отрицательные

)
Здесь, как видно, при
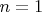
можно выбрать

- параметр, тогда
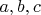
- три последовательных числа, то есть тривиальное решение.
Вывод 3. Трехчлен ранга 3 и больше задается парой чисел  таких, что
таких, что  - полный квадрат.Пример.
- полный квадрат.Пример.Пусть

, тогда требуется разложение на множители числа

. Выберем

.
Тогда

. Дискриминанты соответствующих трехчленов:

, а коэффициенты первого трехчлена - 151, 5694. В обратном порядке -149, 5394
Таким образом, мы получаем две тройки трехчлена с целыми корнями (в чем несложно убедиться):






------
Что же происходит для ранга 4? В первую очередь надо заметить, что такой трехчлен тоже задается парой

, но только не всякой, а при условии, что

- тоже полный квадрат.
Формализовать в общем виде здесь уже не удалось, а перебором "в лоб" находится множество пар.
Например, (4, 10), (5, 44), (18, 34) и т.д.
Перебор где-то к исходу второй тысячи начинает спотыкаться о недостаток разрядов (когда дискриминанты становятся близкими к

, а потом превышают лимит), поэтому далеко уйти не удается.
Но в этом ряду для некоторых случаев прослеживается закономерность, и вот тут начинается
самое необычное!
Пусть

. Как несложно убедиться,

- полный квадрат, и мы можем записать выражения для корней первых трех дискриминантов:



Если теперь раскрыть выражение

, то обнаружится, что корень извлекается:
 Вывод 4. Некоторые полностью целочисленные трехчлены четвертого ранга можно задать всего лишь одним числом
Вывод 4. Некоторые полностью целочисленные трехчлены четвертого ранга можно задать всего лишь одним числом  .
.По формулам выше можно записать в явном виде коэффициенты:


Или:


При подстановке

получаются тривиальные трехчлены.
При

:

(убедитесь, что ранг этого трехчлена действительно 4).
Можно еще обратить внимание, что

, а

, если рассмотреть подробно, то дискриминанты соответствующих трехчленов те же, только расположены в обратном порядке.
Так, для

получается

.
Более высокие ранги.Очевидно, что, если существуют, то они являются продолжением некоторых последовательностей для четвертого ранга. Можно показать, что последовательности, характеризуемые

, ни при каких его значениях не дадут пятый дискриминант квадратом - кроме, конечно же, тривиальных случаев.
Здесь задача приходит к следующей формулировке:
Решите в целых числах систему уравнений:


Тривиальное решение -

, но существуют ли еще?
Сгенерировать

легко - по алгоритму, аналогичному приведенному для третьего ранга. А дальше - узнать среднее арифметическое от квадратов каждой пары

, вычесть из него 1 и выяснить, являются ли полученные числа полными квадратами. Вот тут ничего путного не складывается. Перебор, как уже выше сказано, затыкается и ничего не находит.
Заключение.Среди приведенных целочисленных квадратных трехчленов с целочисленными корнями находятся такие, что, при увеличении коэффициентов на единицу их корни остаются целыми. В некоторых случаях эту процедуру можно проделать дважды, и есть формальный алгоритм подбора коэффициентов. Даже - трижды, для части решений возможна параметризация всего лишь одним параметром. Существуют ли трехчлены, для которых процедуру можно повторить ровно четыре раза - пока неизвестно. Дополнение.Задачу заменой

можно переформулировать так, что меняется только коэффициент при первой степени, но это тоже сводится к поиску дискриминантов.
А тогда графически задача формулируется так: дана парабола
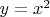
сдвинута так, что она пересекает ось абсцисс в целых точках. Сколько прямых вида

пересекут ее в целых узлах координатной сетки?