док-во несуществования некоторой эллиптической кривой
Нет. Вейль доказал, что если ВТФ неверна, то для кривой Фрея не выполняется одно свойство. Уайлс доказал, что для всех эл. кривых одного типа (куда входит и кривая Фрея) выполняется это свойство. Года через 2 доказали, что это свойство выполняется для вообще всех эл. кривых (это утвердение называлось гипотезой Таниямы-Шимуры-Вейля).
Доказательство несуществования некоторой эллиптической кривой - это док-во взаимно исключающих утверждений:
1. эллиптическая кривая вида

, где

- взаимно простые числа является модулярной.
2. Кривая Фрея не является модулярной.
Кривая Фрея

,
где

, а

- натуральные попарно взаимно простые числа,
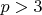
- простой показатель. Факт, что кривая Фрея не является модулярной, доказал Рибет.
Уайлс доказал, что кривые вида

, где

- взаимно простые числа являются модулярными.
Поэтому, если

, то такая эллиптическая кривая модулярна.
Следовательно, эллиптической кривая Фрея не существует, она - фантом, призрак. Ее существование обусловлено только тем, что уравнение Ферма имеет решение.
Подробности см. в книге (стр. 385-393:
Рибенбойм П. Последняя теорема Ферма для любителей(М.: МИР)
http://www.vixri.com/d/Ribenbojm%20P.%20_Poslednjaja%20teorema%20Ferma.pdfТам же: "Некоторые математики не удовлетворены методом доказательства, использующим эллиптические кривые и модулярные формы, которые рассматриваются (вероятно, несправедливо? или
справедливо?) как чуждые этой проблеме."