Я хотел спросить: в первом случае базисными неизвестными будем считать

, а свободными неизвестными

или
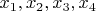
- базисные, а

- свободными?
Соответственно, во-втором:
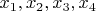
-базисные неизвестные, а

- свободными неизвестными или

- базисные неизвестные, а

-свободными неизвестными?