Вопрос по задаче о гипервещественных числах

[Turfur]

Здравствуйте!
Я читал книгу Голдблатта "Lectures on the Hyperreals", и у меня возник вопрос по упражнению 5.9. Задача состоит в том, чтобы, используя существование тени (т.е. вещественного числа, бесконечно близкого к данному числу) у всех ограниченных гипервещественных чисел, доказать непрерывность множества вещественных чисел в смысле Дедекинда. Т.е. необходимо доказать, что для любого непустого ограниченного сверху множества $A \subset \mathbb R$ найдется точная верхняя грань, используя только указанный факт, но не свойства самих вещественных чисел. В отличие от всех остальных задач этой же главы, мне не удалось ее решить не прибегая к "внутреннему строению" гипервещественных чисел. Сама задача разбита на три пункта, которые предлагается доказывать последовательно. Как я решал:

1. В первом пункте предлагается рассмотреть для каждого $n$ такое минимальное $s_n \in \mathbb Z$, что $s_n / n$ - верхняя грань множества $A$. Необходимо доказать, что такое $s_n$ существует. Я не знаю, почему такое простое утверждение было выделено в отдельный пункт, честно говоря. Пропускаю доказательство, т.к. тут все очевидно.
   
2. Пусть $N$ - неограниченное гипернатуральное число. Тогда необходимо доказать, что $s_N / N$ - ограничено. Для исходной последовательности $\forall n \in \mathbb N \quad a \leqslant s_n / n \leqslant s_1$, где $a \in A$, ведь в качестве $s_n$ всегда можно взять $n s_1$, и тогда $ n s_1 / n = s_1$. По принципу перехода получаем $\forall n \in \mathbb {^\ast N} \quad a \leqslant s_n / n \leqslant s_1$, и, в частности, $a \leqslant s_N / N \leqslant s_1$. Поскольку у всех ограниченных гипервещественных чисел есть тень, можно положить тень $s_N / N$ равной $L$.
   
3. Необходимо доказать, что $L$ - точная верхняя грань $A$. В этом пункте $x \simeq y$ будет означать, что $x - y$ - бесконечно малая. Ранее было доказано утверждение, что если $b, c \in \mathbb R$, то из $b \simeq x \leqslant y \simeq c$ следует $b \leqslant c$, так что то, что $L$ есть верхняя грань, очевидно. Остается доказать, что она наименьшая. Мое доказательство таково: $\forall n \in \mathbb N \quad \exists a \in A \quad (s_n - 1) / n < a $, значит по принципу перехода получаем $\forall n \in \mathbb {^\ast N} \quad \exists a \in {^\ast A} \quad (s_n - 1) / n < a $. В частности $\exists a \in {^\ast A} \quad (s_N - 1) / N < a $. Заметим, что $(s_N - 1) / N = s_N / N - 1 / N$, притом $1 / N$ - бесконечно малая. Имеем $(s_N - 1) / N \simeq s_N / N \simeq L $ и $(s_N - 1) / N < a < s_N / N$, а значит $a \simeq L$. Вот тут - вся загвоздка. Я рассмотрел $a$ как последовательность вещественных чисел, такую, что почти все элементы принадлежат $A$. Из $a \simeq L$ следует, что для любого $\varepsilon > 0$ почти все элементы нашей последовательности отличаются от $L$ не более чем на $\varepsilon$. Поскольку пересечение двух элементов фильтра - тоже элемент фильтра, выходит, что почти все элементы одновременно принадлежат $A$ и меньше $L$ не более чем на $\varepsilon$ (могут быть и равны). Это, в частности, показывает, что такие элементы вообще существуют для любого $\varepsilon$, что и означает, что $L$ - точная верхняя грань.

В последнем пункте пришлось апеллировать к самой конструкции гипервещественных чисел, в то время, как практически все остальное в этой главе можно доказать без этого. Можете намекнуть, есть ли тут какой-то способ сделать это проще?

[Turfur]

Все, решил. Все оказалось безумно просто!
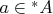
Рассмотрим с того момента, когда мы уже знаем, что $L$ - верхняя грань $A$ и существует $a \in {^\ast A}$ такой, что $a \simeq L$; необходимо доказать, что $L$ - точная верхняя грань $A$. Зафиксируем $\varepsilon \in \mathbb R^+.$. Раз $a \simeq L$, то, очевидно, $\exists a \in {^\ast A} \quad L - a < \varepsilon$. Тогда по принципу перехода, $\exists a \in A \quad L - a < \varepsilon$. Причем это верно для всех $\varepsilon \in \mathbb R^+$! Значит $L$ и вправду точная верхняя грань.
Просто я никак не мог догадаться не включать "$\forall \varespilon \in \mathbb R^+$" в формулу, которую "переносим". Это, похоже, вообще распространенный прием при работе с гипервещественными числами. Собственно, я просто продолжил читать книгу, и в главе про пределы использовался аналогичный трюк.