mihaild, да, действительно, эти множества не обязаны совпадать, ведь функции из

"несут" всевозможные подмножества

, в то время как нам нужны функции, которые будут "нести" эти подмножества не разом, а "по одному".
Попробую так.
Доказательство.Если

, тогда функция,

это та же самая функция, что

, так на всех значениях
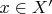
они принимают одинаковые значения.
Тогда рассмотрим множество всех подмножеств множества

-

. Каждый элемент

этого множества заменим на

по аксиоме замены, так как любому множеству отвечает только одно множество всевозможных функций из него. Значит мы получили множество вида

. Теперь по аксиоме объединения мы можем получить множество, состоящее из всех элементов

, а значит мы доказали, что множество всех частичных функций действительно является множеством.
 Вопрос.
Вопрос.Помимо проверки корректности этого доказательства, хотел бы спросить, могу ли я вообще говорить, что если

, то это та же самая функция, что и

? Просто Тао определяет равенство только тех функций, что имеют одинаковые области определения и значений, но я не очень понимаю, что нам мешает определить равенство

и

, ведь это одни и те же функции в том смысле, что они совпадают на всей области определения, так почему бы их не отождествить?
Или это приводит к противоречиям?
-- 12.12.2019, 04:21 --Добавление.Наверное, можно обойтись без каверкания равенства функций.
Возьмём просто множества

и

и произвольные элементы

,
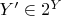
.
Для начала образуем множество

. Оно существует по имеющейся аксиоме. Далее будем по аксиоме парного объединения объединять все множества

, получим множество

, элементы которого - все функции вида

. На него и заменим по аксиоме замены наше

из

. Проделаем этот процесс для всех

. Получим множество из всех множеств функций из

. А далее воспользуемся аксиомой объединения и получим необходимое нам множество частичных функций.

Это рассуждение верно?