Кулоновский потенциал и функция Грина

[DismasK]

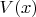
Известно, что кулоновский потенциал $V(x)$ можно получить через функцию Грина. Мне нужно наоборот.

$V(\vec{x})=\frac{e^2}{4\pi\vec{x}}$.
Я попытался обратные преобразования Фурье:

$\tilde{V}(\vec{p})=\int\limits \frac{e^2}{4\pi\vec{x}(2\pi)^3}e^{-i \vec{p}\vec{x}}d\vec{x}$.

Если выбрать вектор $x$ за ось $z$, то переходя к сферическим координатам:

$\tilde{V}(\vec{p})=\int\limits_{0}^{\infty}\int\limits_{0}^{2\pi}\int\limits_{0}^{\pi}\frac{e^2r^2\sin(\theta)}{4\pi r\cos(\theta)(2\pi)^3}e^{-i prcos(\theta)}dr d\varphi d\theta=\int\limits_{0}^{\infty}\int\limits_{0}^{\pi}\frac{e^2r\sin(\theta)2\pi}{4\pi \cos(\theta)(2\pi)^3}e^{-i prcos(\theta)}dr d\theta$.

Дальнейшее вычисление интеграла вызывает трудности. Если использовать замену $t=\cos(\theta)$, то получаю интеграл:
$\int\limits_{-1}^{1}\frac{e^{-iprt}}{t}dt$, решение которого - сумма бесконечного ряда.
Может, я неправильно перешел к сферическим координатам? Или нужно найти другую замену?

[Alex-Yu]

DismasK в сообщении #1429331 писал(а):

Кулоновский потенциал и функция Грина

Известно, что кулоновский потенциал $V(x)$ можно получить через функцию Грина. Мне нужно наоборот.

$V(\vec{x})=\frac{e^2}{4\pi\vec{x}}$.

Во-первых, о какой функции Грина идет речь? Функции Грина разные бывают.

Во-вторых, в приведенной формуле вы что-то странное написали: что такое деление на вектор никому пока что не было известно.

Далее формулы тоже более чем странные.