интегралы помогите решить

[daniilsergeich]

a) какую из подстановок целесообразно исползовать для замены переменной в интеграле tg^3 *фdф
1.t=tg^ф
2.t=tg^2*ф
3.ф=tgt
4.ф=tg^3 *t
5.ф=arctg *t


b)какую из подстановок целесообразно исползовать для замены переменной в интеграле e^x*dx/3+4e^x
1.x=e^t
2.x=4e^t+3
3.t=3+4e^x
4.t=4e^x
5.(3+4e^x)^-1

c)какое из выражение целесобразно принять за и при интегрировании по частям интеграла x^2*e^3x*dx
1.u=x
2. u=e^x
3.u=x^2
4.u=e^3x
5.u=x^2*e^2x


d)интеграл x*arctgx*dx решить немогу

[AD]

daniilsergeich писал(а):

tg^3 *фdф

Что это за ужас такой? Типа $\tg^3$ умножается на $\varphi\,d\varphi$?

daniilsergeich писал(а):

e^x*dx/3+4e^x

А здесь интегрируется только первое слагаемое?


Даже если я правильно понял условие, то:

a) не вижу разницы между 1 и 5; оба ответа меня лично устраивают.
b) здесь вообще всё в лоб считается, никакие замены не нужны
c) не знаю, которая из них "и"

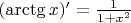
d) По частям считается, производная от арктангенса $(\arctg x)'=\frac1{1+x^2}$ - рациональная функция, а дальше вообще делать нечего.

[Sherpa]

неужели сложно в техе написать???

[AD]

Sherpa писал(а):

неужели сложно в техе написать???

Судя по глубине вопросов, учить тех ради одного раза не стоит ...

[Echo-Off]

daniilsergeich писал(а):

какое из выражение целесобразно принять за и при интегрировании по частям

AD писал(а):

не знаю, которая из них "и"

И вот, я включаю свои телепатические способности... и вижу! Вижу! Вижу, что в исходном задании написано "Какое из выражений целесообразно принять за $u$ при интегрировании по частям".

[bot]

Echo-Off писал(а):

Какое из выражений целесообразно принять за $u$ при интегрировании по частям?

Да уж, не повезло буквам $u$ и $v$ - угораздило же их попасть в формулу интегрирования по частям.
А случись брать, к примеру, $\int ue^udu$ так и вовсе беда.

[PAV]

[mod="PAV"]Тема переносится в карантин. Исправьте в своем сообщении формулы в соответствии с правилами форума (инструкция здесь). Когда будет готово, сообщите любому модератору, и тема будет возвращена обратно.[/mod]