помощь в TEXе

[David 1990]

помогите пожалуйста. Работаю в этой программе впервые. Нужно набрать 54 стр Ландау
\documentclass{article}
\usepackage[utf8]{inputenc}
\usepackage[english, russian]{babel}
\usepackage[T1, T2A]{fontenc}
\begin{document}
Условие равновесия деформированного тела можно сформулировать как условие минимальности суммы электростатической и упругой энергии. Первая из них согласно формулам (2,12), (4,26) равна

$$\upsilon _{\text{Эл}}= (-\frac{V}{8\pi n}) \varepsilon^{2} \approx (-\frac{3V}{8\pi}) \varepsilon ^{2}-(\frac{3V}{10\pi }\frac{a-b}{R})\varepsilon ^{2},$$

где $R$ — первоначальный радиус шара, $a$ и $b$ — полуоси эллипсоида, а

$$ n\approx \frac{1}{3}-\frac{4}{15}\frac{a-b}{R}$$

— коэффициент деполяризации (см. (4,33)).
В силу аксиальной симметрии деформации (вокруг направления поля — оси $х$) отличны от нуля лишь компоненты $u_{xx}$ и $u_{yy}$=$u_{zz}$ тензора деформации. Поскольку мы рассматриваем равновесие по отношению к изменению формы, можно считать при этом объем неизменным, т. е. $u_{ii}=0$. Поэтому упругую энергию можно написать в виде

$$\upsilon_{\text{упр}}=\frac{V}{2}u_{ik}\sigma_{ik}=\frac{V}{3}\left ( \sigma _{xx}-\sigma _{yy} \right )\left ( u_{xx}-u_{yy} \right),$$

где $\sigma _{ik}$ — тензор упругих напряжений (см. VII § 4). Имеем

$$\sigma _{xx}-\sigma _{yy}= 2\mu \left ( u_{xx}-u_{yy} \right ),$$

где $\mu $ — модуль сдвига вещества, а $\sigma _{xx}-\sigma _{yy}= \frac{a-b}{R}$. Поэтому

$$\upsilon_{\text{упр}}= \frac{2\mu (a-b)^{2}}{3R^{2}}V.$$

Минимизируя сумму $\upsilon_{\text{упр}}+\upsilon _{\text{эл}}$ по $a-b$ , получим

$$\frac{a-b}{R}= =\frac{9}{40\pi\mu }\varepsilon ^{2}.$$

5. Найти связь между частотой и длиной волны, распространяющейся по заряженной плоской поверхности жидкого проводника (в поле тяжести). Получить условие устойчивости этой поверхности (Я. И. Френкель, 1935).
Р е ш е н и е. Пусть волна распространяется вдоль оси $x$, ось $z$ направлена вертикально вверх. Вертикальное смещение точек поверхности жидкости $\xi =\alpha exp\left [ i(kx-\omega t) \right ].$ При неподвижной поверхности напряженность поля над ней $E_{z}= E=4\pi\sigma _{0}$, а его потенциал $\varphi=-4\pi \sigma _{0}z$, где $\sigma_{0}$ — поверхностная плотность зарядов. Потенциал поля над колеблющейся поверхностью пишем в виде

$$\varphi=4\pi \sigma _{0}z+\varphi_1, \varphi_1=const\cdot e^{i(kx-\omega t)}e^{-kz},$$

где $\varphi_{1}$— малая поправка, удовлетворяющая уравнению $\bigtriangleup \varphi_{1}=0$ и обращающаяся в нуль при $z\rightarrow 0$ . Вдоль самой поверхности проводника потенциал должен иметь постоянное значение, которое принимаем за нуль; отсюда

$$\varphi\left \right |_{z=0}=4\pi \sigma _{0}\xi.$$

$$\frac{E^{2}}{8\pi}\approx 2\pi \sigma_{0}^{2}+k \sigma _{0}\varphi_{1}\right \|_{z=0}=2\pi \sigma_{0}^{2}+4\pi\sigma_{0}^{2}k\xi.$$

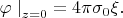
Согласно (5,1) на заряженную поверхность жидкости действует дополнительное отрицательное давление, равное, с точностью до членов первого порядка по $\varphi_{1},$
Постоянный член $2\pi \sigma _{0}^2$ несуществен (его можно включить в постоянное внешнее давление).
\end{document}
вот что получилось, но ошибок много и разобраться до конца не могу

[Утундрий]

(Оффтоп)

David 1990 в сообщении #1425606 писал(а):

помогите пожалуйста. Работаю в этой программе впервые. Нужно набрать 54 стр Ландау

О, теперь я знаю как переиздавали ЛЛ...

[Red_Herring]

David 1990 в сообщении #1425606 писал(а):

но ошибок много и разобраться до конца не могу

Где много? В вашей прогонке или на форуме?
Обратите внимание как нужно оформлять источники в TeX.

[David 1990]

В моей прогонке. А так вроде и не плохо

[Pphantom]

Тема перемещена из форума «TeXнические обсуждения» в форум «Карантин»
по следующим причинам:

- оформите код с помощью соответствующего тэга;
- перед этим внимательно посмотрите на места, в которых форумный движок нашел синтаксические ошибки, скорее всего, часть ваших вопросов это позволит снять.

Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.