Доказательство четырех равенств из комбинаторики

[innokentijglum]

Здравствуйте, форумчане!

Нужна помощь с доказательством четырех равенств из комбинаторики. Вообще, они почти очевидны, но преподаватель говорит, что нужно полное доказательство "step-by-step", а с этим у меня проблемы...

Дано множество из $n$ элементов $S=\{o_1, \ldots, o_n\}$ и 2 разбиения: $X = \{X_1, \ldots, X_k\}$ на $k$ подмножеств, и $Y = \{Y_1, \ldots, Y_l\}$ - разбиение $S$ на $l$ подмножеств, определим следующие числа:

$A_{11}$ - количество пар элементов из $S$, которые в одном и том же подмножестве разбиения $X$ и в одном и том же подмножестве разбиения $Y$
$A_{00}$ - количество пар элементов из $S$, которые в разных подмножествах разбиения $X$ и в разных подмножествах разбиения $Y$
$A_{10}$ - количество пар элементов из $S$, которые в одном подмножестве разбиения $X$ и в разных подмножествах разбиения $Y$
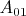
$A_{01}$ - количество пар элементов из $S$, которые в разных подмножествах разбиения $X$ и в одном подмножестве разбиения $Y$

Также обозначим:
$N_{i,j} = |X_{i} \cap Y_{j}|$ - количество элементов в пересечении $X_{i}$ и $Y_{j}$
$A = {n \choose 2} = \frac{n(n-1)}{2}$ - общее количество пар для $S$
$Q_{X} = \sum_{i}{X_{i} \choose 2}$
$Q_{Y} = \sum_{j}{Y_{j} \choose 2}$

Нужно доказать, что:
1. $A_{11} = \sum_{i,j}{N_{i,j} \choose 2}$
2. $A_{00} = A - Q_{X} - Q_{Y} + A_{11}$
3. $Q_{X} = A_{11} + A_{10}$
4. $Q_{Y} = A_{11} + A_{01}$

Напишите, пожалуйста, доказательство, как можно подробнее!

Вроде как, первое равенство - и так понятно, что мы можем набрать пары, которые объединены в $X$ и в $Y$ только для элементов из пересечения $X_{i} \cap Y_{j}$, а второе - есть формула включения исключений. Но такое доказательство не подходит!

Заранее спасибо!

[Lia]

Тема перемещена из форума «Помогите решить / разобраться (М)» в форум «Карантин»
по следующим причинам:


- отсутствуют собственные содержательные попытки решения задач(и).

Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.