Рассмотрим элементарный участок спирали длиною

. Cначала для простоты будет считать что в процессе деформации спирали угол наклона витков к горизонту пренебрежимо малым (линейная теория). Тогда можно считать, что радиусы

и

, проведенные от оси симметрии спирали к центрам торцевых сечений этого участка спирали лежат в одной плоскости и имеют общую точку
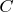
. После деформации кручения второе сечение поворачивается относительно первого на угол

, где

- модуль сдвига (модуль жесткости);

- постоянная кручения;

-крутящий момент. При этом радиус

повернется относительно радиуса

на тот же угол

, а второй конец сечения сместится вниз на расстояние

, где

-радиус витков спирали. Интегрируя обе части этого равенства, получим:

. Проблемы у меня возникают для случая геометрически больших деформаций, когда радиус и угол наклона витков не остаются постоянными. Для этого случая все монографии, что я нашел, утверждают, что отношение

равно изменению кручения пространственной кривой (спирали):

. Здесь

текущий угол наклона. Я пробовал вывести это равенство, используя подход описанный вначале, но не смог. Да, в этом случае

, но откуда взялся

???? И как они разобрались с переменным радиусом???. Прощу Вашей помощи