Открытость вещественно аналитического отображения

[Alexzord]

Пусть $E,F$ - банаховы пространства, $f: E \rightarrow F$ - локально вещественно аналитический изоморфизм в каждой точке $E$.

(Определения:

1) аналитическое = непрерывно дифференцируемо в смысле Фреше,

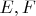
2) вещественно аналитическое: пусть $E, F$ - банаховы, $\mathbb{C}E, \mathbb{C}F$ - их комплексификации, $U \subset E$ открыто. Отображение $f: U \rightarrow F$ называется вещественно аналитическим на $U$, если в каждой точке $U$ найдется окрестность $V \subset \mathbb{C}E$ и аналитическое отображение $g: V \rightarrow \mathbb{C}F$, такое, что $f = g$ на $U\cap V$.)

Вроде бы из этого должно следовать, что $f$ открыто (переводит открытые множества в открытые). Это верно и почему?

[DeBill]

Alexzord
А разве открытость уже не следует из

Alexzord в сообщении #1423911 писал(а):

локально ... изоморфизм

?

[Alexzord]

DeBill в сообщении #1423988 писал(а):

Alexzord
А разве открытость уже не следует из

Alexzord в сообщении #1423911 писал(а):

локально ... изоморфизм

?

Ну наверное, что-то типа "локально непрерывный изоморфизм" уже даст открытость. Пусть $U$ открыто, $y \in f(U)$. Возьмем какой-нибудь $x \in f^{-1}(y) \cap U$. Знаем, что в некоторой окрестности $U_0 \ni x$ отображение $f$ должно быть гомеоморфизмом (непрерывным в обе стороны), значит и открытым, и $f(U_0)$ открыто и является окрестностью $y$, т.е. $y$ - внутренняя точка и $f(U)$ открыто.

Верно?