Q3. What calculation is Google planning to do, or has it already done, that’s believed to be classically hard?
So, I can tell you, but I’ll feel slightly sheepish doing so. The calculation is: a “challenger” generates a random quantum circuit
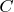
(i.e., a random sequence of 1-qubit and nearest-neighbor 2-qubit gates, of depth perhaps
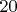
, acting on a 2D grid of
to
qubits). The challenger then sends
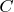
to the quantum computer, and asks it apply
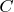
to the all-0 initial state, measure the result in the
basis, send back whatever
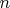
-bit string was observed, and repeat some thousands or millions of times. Finally, using its knowledge of
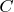
, the classical challenger applies a statistical test to check whether the outputs are consistent with the QC having done this.
So, this is not a problem like factoring with a single right answer. The circuit
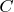
gives rise to some probability distribution, call it DC, over
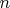
-bit strings, and the problem is to output samples from that distribution. In fact, there will typically be
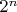
strings in the support of DC—so many that, if the QC is working as expected, the same output will never be observed twice. A crucial point, though, is that the distribution DC is not uniform. Some strings enjoy constructive interference of amplitudes and therefore have larger probabilities, while others suffer destructive interference and have smaller probabilities. And even though we’ll only see a number of samples that’s tiny compared to
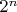
, we can check whether the samples preferentially cluster among the strings that are predicted to be likelier, and thereby build up our confidence that something classically intractable is being done.
So, tl;dr, the quantum computer is simply asked to apply a random (but known) sequence of quantum operations—not because we intrinsically care about the result, but because we’re trying to prove that it can beat a classical computer at some well-defined task.
упрощается и ищут, то число которое она выпадает чаще всего на всём диапазоне ![$X=[0;2^{53}]$](https://dxdy-02.korotkov.co.uk/f/d/4/c/d4c0c02ba3d7dadec640f9417d32181982.png "$X=[0;2^{53}]$")
.
сортируют и группируют по диапазонам и ищут диапазон с максимальным числом повторов.
years, still no quantum computer has even once been used to solve any problem faster than your laptop could solve it, or at least not in any way that depended on its being a quantum computer. In a post-quantum-supremacy world, that’s no longer the case. A superposition involving 
or 
complex numbers has been computationally harnessed, using time and space resources that are minuscule compared to ![$Pr[C \text{ outputs } s_i]$](https://dxdy-04.korotkov.co.uk/f/7/4/0/74053101c1114a18d407403b37bbea5c82.png "$Pr[C \text{ outputs } s_i]$")
over all the samples 
that the QC returned, and then to declare the test a “success” if and only if the sum exceeds some threshold—say, 
, for some constant b strictly between 1 and 2.
time. Is that a showstopper? No, not if 
, and you’re Google and are able to handle numbers like 
, which exceeds a googol, har har). By running a huge cluster of classical cores for (say) a month, you can eventually verify the outputs that your QC produced in a few seconds—while also seeing that the QC was many orders of magnitude faster. However, this does mean that sampling-based quantum supremacy experiments are almost specifically designed for 
-qubit devices like the ones being built right now. Even with 
qubits, we wouldn’t know how to verify the results using all the classical computing power available on earth.
-digit number, it would be easy to check the result by simply multiplying the claimed factors and running a primality test on them. Likewise, if a QC were used to simulate some complicated biomolecule, you could check its results by comparing them to experiment.)
).