Здравствуйте!
Пусть

равномощно подмножеству

множества

, а

равномощно подмножеству

множества

. При взаимно однозначном соответствии между

и

подмножество

переходит в некоторое подмножество
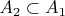
. При этом все три множества

,

и

равномощны, — и нужно доказать, что они равномощны множеству

, или, что то же самое,

.
Пусть

— функция, осуществляющая взаимно однозначное соответствие

(элемент

соответствует элементу
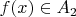
). Когда

переходит в

, меньшее множество

переходит в какое-то множество
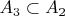
. Аналогичным образом само

переходит в некоторое множество

. При этом
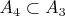
, так как

. Продолжая эту конструкцию, мы получаем убывающую последовательность множеств

и взаимно однозначное соответствие

, при котором

соответствует

. Формально можно описать
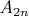
как множество тех элементов, которые получаются из какого-то элемента множества

после

-кратного применения функции

. Аналогичным образом
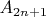
состоит из тех и только тех элементов, которые получаются из какого-то элемента множества

после

-кратного применения функции

. Заметим, что пересечение всех множеств

вполне может быть непусто: оно состоит из тех элементов, у которых можно сколько угодно раз брать

-прообраз. Теперь можно сказать так: множество

мы разбили на непересекающиеся слои

и на сердцевину

.
Часть доказательства до места, где мне становится непонятно, а именно последние 2 предложения:
1) "можно сколько угодно раз брать

-прообраз". Что во что отображается ?
2)

, не ясно как можно его получить, если

не кончаются ?