Численный расчет выражения

[Jiggy]

Приветствую. Сразу сформулирую задачу.

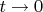
Есть выражение $\frac{e^{-\sigma^2t} - 1 + \sigma^2t}{\sigma^4t^2}$, $\sigma > 0$. Нужно рассчитать выражение при $t \to 0$ и при $t = 0$.

В случае $t = 0$ наиболее логичным считаю разложить экспоненту в ряд Маклорена в точке $t=0$ до $t^2$ включительно.
То есть: $e^{-\sigma^2t} = 1 - \sigma^2t + \sigma^4t^2/2 + O(t^3)$. Таким образом, cократив дробь, получим: $0.5 + O(t)$, что равняется 0.5.

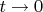
В случае же $t \to 0$ пытаюсь посчитать обычный предел. У нас неопределенность 0/0, поэтому можно пролопитировать, насколько я понимаю. Беря производную от числителя и знаменателя по t, получаем: $\frac{-\sigma^2e^{-\sigma^2t} + \sigma^2t}{2\sigma^4t}$. И получаем в пределе $\inf$, но вольфрам этот предел рассчитал, как 1/2, разложив в ряд Маклорена числитель.

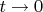
Получается, что в ряд Маклорена нужно раскладывать в случае $t \to 0$, а не при $t=0$? В таком случае, как считать это выражение непосредственно в точке $t=0$?

Заранее спасибо.

[wrest]

Jiggy в сообщении #1422558 писал(а):

В таком случае, как считать это выражение непосредственно в точке $t=0$?

Никак, потому что на ноль делить не можно.

[wrest]

Jiggy в сообщении #1422558 писал(а):

И получаем в пределе $\inf$, но вольфрам этот предел рассчитал, как 1/2,

Видимо, ошибка где-то, помойму предел не существует. Проверьте "лопитирование".

[Jiggy]

wrest

Такое выдал вольфрам.


Исходное условие задачи такое.


Может быть я некорректно хочу решить задачу?

-- 27.10.2019, 00:44 --

В лопитировании описка: в числителе не убрал t во втором члене, но тем не менее лопиталь приводит к C/\inf.

[wrest]

Jiggy в сообщении #1422575 писал(а):

Такое выдал вольфрам.
Изображение

Это верно.

-- 27.10.2019, 00:55 --

wrest в сообщении #1422576 писал(а):

Может быть я некорректно хочу решить задачу?

А, ну так тут, как говорится, на ваш выбор. Это ж не вопросы к математике, а скорее к программированию, как мне кажется.

Jiggy в сообщении #1422575 писал(а):

В лопитировании описка: в числителе не убрал t во втором члене, но тем не менее лопиталь приводит к C/\inf.

Не, ну чего вы Лопиталя так обижаете... Нет там бесконечностей, предел равен $1/2$
Лопитируйте пока это не станет уже слвсем очевидно.

[arseniiv]

О, авторы вопроса как минимум намекают на использование функции expm1.

[Jiggy]

числитель: $(e^{-\sigma^2t}-1+\sigma^2t)' = -\sigma^2e^{-\sigma^2t} + \sigma^2$. Неужели я неправильно дифференцирую? Если wrest прав, то здесь закралась одна ошибка.

Сейчас осознал, что мы можем второй раз дробь лопитировать, так как и числитель, и знаменатель стремятся к 0 при $t \to 0$. И после этого как раз получается 0.5. Хорошо, предел 0.5.

Получается, что при $t \to 0 $ предел существует и равен 0.5. А непосредственно в точке 0 что делать? Разложить в ряд Маклорена? Тогда также получим 0.5. В итоге в обоих случаях получаем 0.5, но в первом - лопиталь, во втором - Маклорен. Ошибаюсь?

[wrest]

Jiggy в сообщении #1422579 писал(а):

Неужели я неправильно дифференцирую? Если wrest прав, то здесь закралась одна ошибка.

Теперь дифференцируете правильно.
Про вторую это я неправ был (вы ж исправленный вариант не написали, вот я и подумал раз у вас бесконечность все одно выходит значит еще одна ошибка).
Так где ж вы там бесконечность-то увидели? Там опять $0/0$, дифференцировать еще раз надо.

[Jiggy]

wrest, Да, затупил. Еще раз продифференцировал, и все стало ОК.

[wrest]

Jiggy
А в чем, по вашему, вообще суть проблемы и смысл задачи?

[Jiggy]

wrest
Насколько я понимаю, нужно показать, как вычислить выражение в зависимости от $t$ (2 случая) и доказать, что приведенные методы в каждом из случаев, действительно, можно применять.

[Евгений Машеров]

$\frac 1 2 =0.5$
То есть оба решения совпадают. Если, конечно, понимать, что и в "первом решении" переход к пределу, только слегка замаскированный, а во втором решении дифференцировать аккуратнее (и два раза).

[wrest]

Jiggy в сообщении #1422585 писал(а):

Насколько я понимаю, нужно показать, как вычислить выражение в зависимости от $t$ (2 случая) и доказать, что приведенные методы в каждом из случаев, действительно, можно применять.

Мне кажется, что речь идёт о том, как справиться с потерей точности при сложении близких больших чисел. То есть как преобразовать вычисления так, чтобы не получались промежуточные результаты типа $1,000000000000000000000000000000000002334129394$

[arseniiv]

По-моему тоже это не задача «найдите предел двумя способами». Скорее всего про вычисление в нуле имеют в виду доопределённую по непрерывности функцию, её-то нашли, это хорошо, но вторая часть — вычислить как можно лучше (но не лезя на стенку) выражение при $t$, близких к нулю, от которых ожидается, что машинной (или другой заданной) точности хватит, чтобы отличить результат от $0{,}5$, но если находить прямо по формуле, точность сильно потеряется. (Потому я намекнул на expm1.)