Да. И я его вчера засыпая таки выразил. Но это чёрная магия и я бы хотел получить ответ более понятным способом. Чуть позже допишу, что вышло.
-- Сб окт 26, 2019 14:52:42 --(Ещё раз напомню про расстояния: аффинная карта проективного пространства, и введённая евклидова структура на ней, не сохраняются при
всех проективных преобразованиях. Так что конкретные расстояния между парами точек должны быть обходимы. И они есть.)
-- Сб окт 26, 2019 15:41:57 --В общем отрубим всё лишнее, пусть

прямая (а

плоскость). Дальше я решил потребовать, чтобы искомое выражение от векторов, задающих прямые, вообще не менялось при линейных преобразованиях и при растяжении этих векторов по отдельности — вроде второе не совсем необходимо, ну да ладно.
Дальше, внешние произведения у нас могут быть осмысленные в этом случае только двойные, а тройные и далее уже нули; двойные лежат в одном и том же пространстве, можно делить. Возьмём например

: ага, линейные преобразования оставят его как есть, умножаются на определитель и верх, и низ. Но зато нет никакого постоянства при растяжении отдельных

. Можно попытаться домножить на

, но мы законно получим единицу, и вместо того чтобы громоздить решения ещё длиннее, начнём иначе:
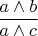
— тогда продолжение удовлетворительное и что-то сильно напоминающее:

(притом это и единственное продолжение, если мы собираемся остановиться лишь на двух дробях, а мы собираемся). Эта величина, теперь мы видим ясно, терпит и линейные преобразования, и совершенно нечувствительна к выбору векторов—представителей своих прямых. И боги, она похожа на

. Давайте проверим, связаны ли они.
Выберем аффинную карту, то есть в данном случае аффинную прямую

(а вообще наши построения останутся инвариантными относительно замен

и

, как и было бы хорошим тоном) и повыбираем

как такие векторы на наших прямых, лежащие на карте, то есть представим их в виде

и т. д., кроме тех прямых, которые совпадают с

— их придётся обрабатывать в формулах отдельно. (Кто потерялся, такая прямая задаёт бесконечно удалённую с точки зрения этой аффинной карты точку.) Их тогда для удобства представим как

и т. д..
Посмотрим теперь на внешние произведения для каждого из трёх случаев:
(1)

представим,

представим:

(2)

представим,

не представим:

(3) оба непредставимы:

Теперь вспомним, что у нас в целом

. Очень неудобно перебирать все случаи, но видно, что если лишь один вектор непредставим, у нас по множителю в числителе и знаменателе сократятся. Если два вектора равны (эквивалентно совпадению проективных точек), то в случае типа
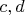
получим ноль, в случае типа

бесконечность, в случае типа

получим единицу, притом не важно, представимы эти совпадающие векторы или нет. Если три совпадают… в общем, рассмотрим лучше случай, когда все векторы представимы, тогда выражение приходит к виду
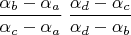
, а ведь эти разности — это и есть расстояния

с точки зрения выбранной карты! Ну, с точностью до умножения на что-нибудь, потому что евклидову структуру я не вводил — мы на прямой и нам нужны лишь отношения, а они определены однозначно, и нечего.
В самом конце остаётся только переставить

так, чтобы они стояли общепринятым образом:

И понять как прийти к формуле не путём кучи догадок. И придумать способ в доказательстве эквивалентности обычному определению не рассматривать кучу случаев с бесконечностями и нулями.