Хочу решить упражнение.
Цитата:
Доказать при помощи теоремы 3, что если

- поле, то группа всех автоморфизмов кольца
![$F[X]$ $F[X]$](https://dxdy-01.korotkov.co.uk/f/8/a/f/8af16aec060ea14e27fde30c150df7f782.png)
, тождественных на

, изоморфна группе преобразований

, где

и

.
Теорема 3
Цитата:
Пусть

и

- произвольные коммутативные кольца,

- элемент из

и

- гомоморфизм. Тогда существует, и притом единственное, продолжение

до гомоморфизма
![$\varphi_t: A[X] \to K$ $\varphi_t: A[X] \to K$](https://dxdy-02.korotkov.co.uk/f/1/1/b/11b44ba440ef9df2a471eb3bd8ceab4782.png)
кольца многочленов
![$A[X]$ $A[X]$](https://dxdy-04.korotkov.co.uk/f/b/1/0/b106b543b5b5c4635b5f1cb75ce8315182.png)
в

, переводящего переменную

в

.
Для начала нужно понять о каких именно объектах в тексте идет речь.
1) С группой всех автоморфизмов кольца
![$F[X]$ $F[X]$](https://dxdy-01.korotkov.co.uk/f/8/a/f/8af16aec060ea14e27fde30c150df7f782.png)
, тождественных на

вроде как все понятно. Это такие автоморфизмы

, у которых

для всех

. (Верно?)
2) А вот что такое группа преобразований

, где

и

пока не ясно.
Группой преобразований называется подгруппа группы всех биективных отображений какого то множества в себя с операцией композиции отображений.
То есть для начала у нас должно быть какое то множество на котором мы будем плодить биективные отображения.
Но что в данном случае является таким множеством?
На сколько я могу понять,

и

тут фиксированы. Ибо если они не фиксированы, то

получается не биективным.
Если

понимать в алгебраическом смысле, то это всего один элемент

и в совокупности с фиксированными

и

дает отображение
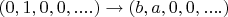
. Тоже ерунда какая то.
Если

понимать в функциональном смысле, то есть как переменную. То в зависимости от кольца

из которого будут браться значения в качестве

, может получиться так, что два разных

отобразятся в одно и тоже значение из

. И соответственно биективность ломается.