Оператор сжатия

[pandemodeus]

Добрый день.
Возникла проблема при решении следующей задачи:
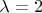
В геометрическом пространстве $V_3$ задана прямоугольная декартова система координат $(O;e_1;e_2;e_3)$. В базисе $e_1,e_2,e_3$ построить матрицу оператора $\mathcal{A}$, если $\mathcal{A}$ осуществляет сжатие с коэффициентом $\lambda=2$ к плоскости $x-2z=0$ параллельно прямой $x=y=z$;
Рассуждаю так:
Прежде всего, найдем направляющие векторы указанных прямой и плоскости. Для прямой: $a_1=(1,1,1)$, для плоскости: $a_2=(2,0,1), a_3=(0,1,0)$. Рассмотрим данный оператор в базисе $a_1,a_2,a_3$. В этом базисе матрица оператора будет иметь вид:

$$\mathrm{A} _{a}=\begin{bmatrix} 1&0 &0 \\ 0&1 &0 \\ 0&0 &2 \end{bmatrix}$$

Столбцы матрицы перехода от ортонормированного базиса к базису $a_1,a_2,a_3$ будут являться координатными столбцами векторов $a_1,a_2,a_3$. Значит, чтобы найти матрицу оператора в искомом базисе, нужно воспользоваться формулой: $\mathrm{A} _{e} = \mathrm{Q}\mathrm{A} _{a}\mathrm{Q}^{-1}$.
Таким образом искомая матрица вычисляется:

$$\mathrm{A} _{e}=\begin{bmatrix} 1&2 &0 \\ 1&0 &1 \\ 1&1 &0 \end{bmatrix}\begin{bmatrix} 1&0 &0 \\ 0&1 &0 \\ 0&0 &2 \end{bmatrix}\begin{bmatrix} -1&0 &2 \\ 1&0 &-1 \\ 1&1 &-2 \end{bmatrix}=\begin{bmatrix} 1&0 &0 \\ 1&2 &-2 \\ 0&0 &1 \end{bmatrix}$$

Однако, ответ не совпадает.
Подскажите, пожалуйста, в чем ошибаюсь?

[arseniiv]

$\mathrm A_a$ — это матрица оператора растяжения в 2 раза, а не сжатия в 2 раза.

[pandemodeus]

arseniiv в сообщении #1420736 писал(а):

$\mathrm A_a$ — это матрица оператора растяжения в 2 раза, а не сжатия в 2 раза.

Да, вы правы, но все равно не сходится, причем на опечатку совсем не похоже.

-- 15.10.2019, 13:04 --

Вопрос закрыт. Ошибка была банальной - неверный порядок векторов в матрице $\mathrm{A}_a$. В моем случае матрица должна иметь вид:

$$\begin{bmatrix} 2&0 & 0\\ 0&1 &0 \\ 0&0 &1 \end{bmatrix}$$