Изменение порядка интегрирования

[Максим 86]

Такая вот интересная тема в контрольной попалась (я заочник). Что делать вообще не знаю. В методичке об этом упомянуто вскользь. Помогите пожалуйста:

Изменить порядок интегрирования и найти полученный кратный интеграл

[Андрей123]

Попробуйте построить область интегрирования.

[Jnrty]

Максим 86, Ваша формула на нашем форуме должна записываться так:

$$\int\limits_{-2}^0dy\int\limits_{-1}^{y+1}\sqrt{x}ydx+\int\limits_0^1dy\int\limits_{-\sqrt{1-y^2}}^{\sqrt{1-y^2}}\sqrt{x}ydx$$

$$\int\limits_{-2}^0dy\int\limits_{-1}^{y+1}\sqrt{x}ydx+\int\limits_0^1dy\int\limits_{-\sqrt{1-y^2}}^{\sqrt{1-y^2}}\sqrt{x}ydx$$

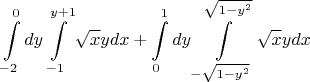
[mod="Jnrty"]Замена формул картинками не разрешается. Замените свою картинку тем кодом, который я привёл, а потом почитайте http://dxdy.ru/viewtopic.php?t=8355 и http://dxdy.ru/viewtopic.php?t=183. Если в дальнейшем будете нарушать правила, тема отправится в "Карантин".[/mod]

Кстати, как совместить отрицательные пределы интегрирования по $x$ с областью определения подынтегральной функции?

[Профессор Снэйп]

Jnrty писал(а):

Кстати, как совместить отрицательные пределы интегрирования по $x$ с областью определения подынтегральной функции?

Может, функции комплекснозначные? Хотя тогда непонятно, какие из ветвей брать.

[antbez]

Я думаю, о комплекснозначности речь идти не может... Обычный пример!

[Henrylee]

antbez писал(а):

Я думаю, о комплекснозначности речь идти не может... Обычный пример!

Тогда надо навесить на $x$ модуль и сделать кирпичом, мол "як и було"

[Максим 86]

Еще вопрос назрел.
"и найти полученный кратный интеграл" = или != "вычислить полученный интеграл"? Сейчас перепроверял работу, оказалось что вычислил с ошибкой. Без ошибки получаются мнимые числа
Очень важно узнать ответ.

[нг]

[mod]перезжаем в Карантин. Jnrty всё сказал.

Пожалуйста, исправьте и сообщите модератору (ЛС).[/mod]