Здравствуйте. Можете, пожалуйста, проверить решение двух задач по теории вероятностей? Только сам метод решений и оформление, вычисления я сам перепроверю.
1) Есть 15 магазинов первого производителя, 10 магазинов второго производителя, 15 магазинов третьего производителя. Вероятность купить бракованный товар в 1 магазине равна 10%, в третьем - 2%. Известно, что вероятность купить бракованный товар во 2 магазине равна вероятности купить бракованный товар в случайно выбранном магазине. Найти эту вероятность.
Пусть вероятность купить бракованный товар во 2 магазине равна

. Тогда вероятность купить бракованный товар в случайном магазине по формуле полной вероятности равна (извините, что пишу так, TeX не отображает русские буквы) P(брак | куплен в 1 магазине)

P(куплен в 1 магазине)

P(брак | куплен в 2 магазине)

P(куплен в 2 магазине)

P(брак | куплен в 3 магазине)

P(куплен в 3 магазине)


. По условию эта вероятность равна

.


2) Биатлонист четыре раза стреляет по мишени, а затем едет на лыжах к финишу. Выстрелы независимы, вероятность попасть равна

. Если он делает 3 или более попадания, вероятность победить равна

. Если он делает 2 или менее попадания, вероятность проиграть равна

. Биатлонист победил. Найти вероятность того, что он сделал не более двух попаданий по мишени.
По формуле Байеса (ещё раз извините за формулы) P(не более 2 попаданий | победа)

P(победа | не более 2 попаданий)

P(не более 2 попаданий)

P(победа)
Найдем вероятность победы, по формуле полной вероятности P(победы)

P(победы | не более 2 попаданий)

P(не более 2 попаданий)

P(победы | не менее 3 попаданий).
Далее

- вероятность сделать

попаданий.
Из свойства аддитивности вероятностей: P(не более 2 попаданий)
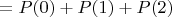
.
По формуле Бернулли

;

;

P (не более 2 попаданий)

.
P (не менее 3 попаданий)

P (победы) =
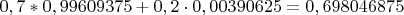
P(не более 2 попаданий | победа)

.