Предел не выглядит трудным, но что-то возник сильный затык на нем.
Найти
![$$\lim_{x\to \infty} \sqrt[3]{(x-1)(x-2)^2} - x$$ $$\lim_{x\to \infty} \sqrt[3]{(x-1)(x-2)^2} - x$$](https://dxdy-04.korotkov.co.uk/f/f/3/8/f381752b7de0178c6339fbb7344587a882.png)
Решаю:
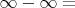
(неопределенность, домножим на сопряженное по формуле
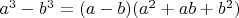
, т.е. на

.
Получаем
![$$\lim_{x\to \infty} \frac{(x-1)(x-2)^2-x^3}{\sqrt[3]{(x-1)^2(x-2)^4}+x\cdot\sqrt[3]{(x-1)(x-2)^2}+x^2}$$ $$\lim_{x\to \infty} \frac{(x-1)(x-2)^2-x^3}{\sqrt[3]{(x-1)^2(x-2)^4}+x\cdot\sqrt[3]{(x-1)(x-2)^2}+x^2}$$](https://dxdy-03.korotkov.co.uk/f/6/c/4/6c4e420424e6fd28f130017873fbb97182.png)
И вот тут я уже не знаю что делать. Вроде получается снова неопределенность, только

. Делю на x в старшей степени, т.е. на

, и.. не понимаю. Как записать происходящее под куб. корнями в знаменателе? Внести туда

, т.е. получить

и почленно поделить выражения с раскрытыми скобками под корнями? Или как-то иначе действовать?
Жду ваших ответов и помощи)