alcoholist, у меня сразу же возник вопрос по определениям в учебнике.
0.
Цитата:
…путь

в (топологическом) пространстве

— это (непрерывное) отображение

, определенное на интервале

. Под интервалом мы понимаем любое связное подмножество вещественной прямой. Оно может быть открытым или замкнутым, ограниченным или неограниченным; множество, состоящее из одной точки, также считается интервалом.
Но потом везде в качестве области определения путей указывается
![$[a, b]$ $[a, b]$](https://dxdy-04.korotkov.co.uk/f/b/d/4/bd4455e79810acc06e3d31c60fb8bfb282.png)
. Так всё-таки любое связное подмножество или замкнутый интервал? Если любое связное подмножество, как определить конкатенацию (умножение) путей?
1. Чтобы доказать, что
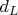
— метрика, надо доказать, что для любого

верно

, а для этого надо доказать, что существует допустимый путь

, проходящий через

. Потом из аддитивности длины пути
![$L(\gamma\restriction [a, a]) = L(\gamma\restriction [a, a]) + L(\gamma\restriction [a, a])$ $L(\gamma\restriction [a, a]) = L(\gamma\restriction [a, a]) + L(\gamma\restriction [a, a])$](https://dxdy-04.korotkov.co.uk/f/f/c/3/fc35305022b291de2c670dcc35f635d782.png)
, где

, я могу вывести
![$L(\gamma\restriction [a, a]) = 0$ $L(\gamma\restriction [a, a]) = 0$](https://dxdy-03.korotkov.co.uk/f/a/4/5/a459484f97251f8d29ca17fcbf1296cc82.png)
. Что-то я не вижу никакой аксиомы, говорящей о существовании допустимых путей. Что, если допустимых путей нет?