THE MATHEMATICAL THREAD IN MY LIFE
BY VLADIMIR KARAPETOFF
[EDITOR's NOTE. - The author of this article was born and educated in Imperial Russia, studied electrical engineering in Germany, and came to this country in 1902. From 1904 to 1939 he was a professor of electrical engineering at Cornell University, now professor emeritus, and throughout his life has been a prolific writer and consultant to many industrial concerns.]
I INHERITED my love for mathematics from my father who was a prominent mechanical engineer. My mother, previous to her marriage, was a mathematics teacher in a high school. My type of mind is essentially synthetic, bent on generalizations and short cuts. All of arithmetic was so easy to me, I just did the problems intuitively long before my time in school. My father encouraged me to go directly over to algebra and geometry, and stimulated my interest g by showing me wonderful relationships here and there. In the familiar type problem about the merchant who bought and sold cloth and made profit, he showed me when I was barely eight) how the number of yards of cloth, the unit price, etc., could be denoted by a, b, c, etc., and numerous problems reduced to typical equations to be solved for the unknown quantities. After this, I looked down on specific numerical problems as something inferior.
Father also challenged me to find a rule for squaring numbers ending on 5, and I brought him the rule
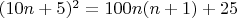
. According to this rule one can write directly that

. I was also thrilled by the properties of Pythagoras' pants, that is, the squares drawn upon the three sides of a right-angle triangle. In this manner, much of my high-school mathematics was anticipated in an unsystematic way and needed only an orderly arrangement later. High-school trigonometry was an inspiring enlargement and unification of algebraic and geometric concepts, although my fluency in it almost cost me my engineering career.
I was sent to St. Petersburg to compete for entrance in the most fashionable Institute of Ways of Communication, where there were at least twenty young men for every vacancy and where the examiners were merciless in order to eliminate as many applicants as possible from the start. I was asked to prove that in any triangle the sum of the trigonometric tangents of the angles was equal to the product of these tangents. I simply wrote from memory the expression for the sine of the sum of three angles, equated it to zero, and divided the result by the product of the cosines. The tired professor glanced at the blackboard hastily and said: "You have no conception of how to go about this problem; rub it off." Although thoroughly trained in military discipline, I said imploringly: "But, professor, let me explain," and in a few words showed him that I had a correct proof. Later I found that those to whom this problem was given usually covered the whole blackboard with formulas, and this fact misled my examiner. I studied analytic geometry and differential calculus under him and owe him a debt of gratitude for the powerful general methods with which I have later been able to build on his foundations.
The school was patterned after the famous French colleges in which noted mathematicians of France received part of their inspiration and training. The experimental and practical parts were subordinated, to theory, and no one who was not fluent with analytic geometry and calculus could hope to master even the purely engineering courses. Descriptive geometry, physics, strength of materials, theory of structures, machine elements, thermodynamics, hydraulics, geodesy, advanced dynamics, electrical engineering, and even such purely applied disciplines as bridges and railroads were largely based on calculus.
After graduation as civil engineer, in 1897, I received an appointment in the Department of Waterways, at the same time holding a part-time instructorship in hydraulics and electrical engineering in my alma mater. This brought me in contact with some partial differential equations of hydrodynamics and electric fields. The problem on which I was working for the government was that of resistance of barges to haulage, for some proposed canals. In view of paucity of experimental data, it required much mathematical study and simplification of unsolvable equations of eddies in viscous liquids. I also came in touch with Poincare's work on probabilities in an effort to I get the most out of the meager and inaccurate experimental data.
The years 1899-1900 were spent in Germany, studying the then new polyphase alternating currents. The theory was not yet well understood, and I eagerly experimented with the available machines, to familiarize myself with the subject qualitatively. Yet my synthetic mind could not rest until I succeeded in deriving some general theorems regarding an

-phase unbalanced system from which the properties of the ordinary symmetrical two- and three-phase systems could be immediately deduced. I got my clues from the statics of structures, Lagrangian equations of motion, properties of simultaneous equations, and whatever other branches of applied mathematics I was familiar with. My work on the subject was later published in German and in Russian.
In 1902 I came to this country and entered the employ of the Westinghouse Electric & Manufacturing Co., in East Pittsburgh, Pennsylvania, remaining there until called to Cornell University in the fall of 1904. While discussing various problems with American engineers, at that time and later, I gradually have come to certain conclusions which have essentially shaped my research and literary activities in the subsequent years. These conclusions are as follows:
1. There would be less waste, more speed, better performance, and better chance for our products on international markets if more mathematics, theoretical physics, and analytical mechanics were used in our industries. It would be impractical (and wasteful if practicable) to give all or many students of engineering more extensive instruction in these disciplines than at present. A "bucket brigade" arrangement, so effective in Germany, should be used much more in this country. I sometimes express this idea in the words "practical practician", "theoretical practician", "practical theoretician", "theoretical theoretician". A practical radio man is troubled with the performance of a vacuum tube and is at the end of his resources as to remedies. He discusses the difficulty with a theoretical practician who feels that the electrons could not be made to move in paths desired by the practical man. He sees the elements and the factors in the problem but cannot express them mathematically. So he strips the problem of the unessentials and lays it before a practical theoretician who expresses the relationships and the desiderata in a mathematical form. However, he is not able to solve the resulting equations, lays the problem before a theoretical theoretician in that particular held of equations, and gets advice as to how to proceed. The problem then travels back and finally reaches the practical practician, perhaps in the form of a few numerical data, a curve, or a simple formula, with which he can proceed with his problem.
2. There is a widespread naive belief among the engineers (the belief being fostered by elementary courses in engineering) that a practical problem can always be solved step by step. You first decide upon the length of a shaft; from this you determine its diameter. Then you compute the size of the flywheel, etc., etc. In reality, this is a problem in simultaneous equations, all the variables being inter-dependent in a rather complicated manner. Not that it is necessary to solve such simultaneous equations formally, rather than proceeding by successive approximations. The important point is for the engineer to see this interdependence clearly. To stimulate this manner of simultaneous design, the writer has developed and built a number of kinematic devices in each of which the interconnected linkages if obey certain equations, thus forming a system of simultaneous equations identical with those which are to be fulfilled in the desired piece of apparatus. The latter may be an electrical machine, but the corresponding kinematic device may be entirely non-electrical, and vice versa.
3. Theoretical achievements outside this country remain unknown to our engineers, or are disregarded by them for long periods of time, to the detriment of the industry, and indirectly of the country at large. The same is true of new branches of mathematics, first proposed for assistance in a new engineering problem. Thus, even plane trigonometry was opposed for alternating currents. Later, complex quantities and hyperbolic functions were sneered at. As a practical man once said to me: "You cannot generate electricity out of the square root of minus one." Conjugate functions, Fourier series, differential equations of damped oscillations, matrices, tensors -- all these had to fight their way into our engineering circles. Often those who had had most to do with the apparatus involved claimed that it could be designed, built, and operated without the newfangled ideas which it would take a lifetime to learn anyway.
As a result of such experiences, I decided that my place in this country's industrial, scientific, and educational fields could best one of a middleman, bringing more branches of mathematics and theoretical physics to the service of engineers and applied physicists, and taking unsolved practical problems to friendly mathematicians. In each case, considerable work of translation and adaptation had to be done, with myself playing the part of a theoretical practician or practical theoretician, or both, as the case may be.
I wish we had more such middlemen and bucket-brigade volunteers. A few large industrial organizations, such as the Bell Telephone System and the General Electric Co., are on a fair way to permanent self-sufficiency, but smaller concerns still are at the stage thus expressed to me by an owner: "I hire a Ph.D. and I prod him to solve my problem; then I fire the Ph.D."
Perhaps too much attention is being paid in colleges to the formal side of equations of curves, differentiation, and integration, to detriment of a broad point of view upon mathematical processes as mode of thinking and powerful tool supplementing our qualitative reasoning. More attention whould be paid to clothing physical economic problems in a mathematical form, so that even those engineers who do not possess the facility of handling equations or functions could exert their influence in drawing more theoretical practicians into the ranks of the industry.
A musician practices scales and exercises as a means to an end. However paradoxical it may seem, I have derived the most benefit in my applied mathematical Work from practicing on such abstract ideas as complex numbers, theory of relativity, and multidimensional spaces. I call this "playing a game." You make certain assumptions and follow them logically to their conclusion, whether or not the results look like our workaday three-dimensional Euclidean world or not.