Вот один из примеров, который так и не удалось свести к чему-то человеческому. Есть система

В первую очередь интересует поведение решения при

и будет физически удовлетворительно, если

хотя бы не растет. Заменой

приходим к
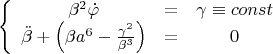
Теперь возьмем (вот сейчас очень необоснованно будет...)

подставим это в

и усредним по интервалу времени, большому для

, но малому для

. Получится

(многоточие означает члены, не пережившие переход к пределу

) и наконец

Откуда находим

Что вполне физически хорошо.
Вот эти-то

и

войдут в частоту (возможно и в трение, смотреть нужно) неких линейных уравнений второго порядка. Конечно, желательно получить их в замкнутом виде, но верится в это слабо.