Пусть

- окружность единичного радиуса с центром в начале координат на комплексной плоскости.
Пусть

- натуральное число,

;


- натуральное число,

.
Пусть

- правильный

-угольник с вершинами на окружности

.
Очевидно, что без ограничения общности можно считать, что его вершины


(

) - комплексные корни

-й степени из единицы, т.е.
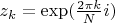
,


.
Рассмотрим теперь
плоский "подмногоугольник" (не обязательно правильный) с

вершинами в точках

.
Множество таких плоских

-угольников обозначим через

.
Можно ли выписать общий вид конформного отображения, переводящего какой-либо фиксированный

-угольник из

на другой

-угольник из

?
Я имею в виду "точное аналитическое" решение данной задачи в "конечном" виде, без использования промежуточного отображения на единичный круг или верхнюю полуплоскость.
Ясно, что достаточно найти общий вид конформного отображения, переводящего
конкретный (например, правильный)

-угольник из

на любой другой

-угольник из

.
Дайте, пожалуйста, ссылки на литературу, если это отражено в книгах.