Число решений

[RgWhite]

Помогите решить!
Найти число точек над полем $F_q$ (q-простое число). Дана кривая $x^2+y^2=1$ и ее параметризация $x=\frac{1-t^2}{1+t^2}, y=\frac{2t}{1+t^2}$
(это меня друг попросил запостить, может я что-то не правильно понял)

[Echo-Off]

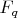
Не понял насчёт параметризации. Предположим, что задача такая: найти число решений $x^2+y^2=1$ над полем $F_q$, где $q$ - простое.

Рассмотрим $q>2$ ($q=2$ можно на пальцах посчитать). При фиксированном $x$ существует $1 + \left(\frac {1-x^2}q\right)$ различных $y$, удовлетворяющих $x^2+y^2=1$. Значит, всего решений у нас будет (обозначим это число $N$)

$$N = \sum\limits_{x=0}^{q-1}\left(1 + \left(\frac {1-x^2}q\right)\right) = q + \sum\limits_{x=0}^{q-1}\left(\frac {1-x^2}q\right)$$

.

Очевидно, что $2\leqslant N \leqslant 2q-2$. Не меньше двух, так как хотя бы два решения есть, и не больше $2q-2$, так как в сумме $\sum\limits_{x=0}^{q-1}\left(\frac {1-x^2}q\right)$ есть хотя бы два слагаемых, равных нулю (соответствующие $x=1$ и $x=q-1$).
Поэтому если мы докажем, что $N\equiv -\left(\frac {-1}q\right) \pmod{q}$, то отсюда будет следовать, что $N = q-\left(\frac{-1}q\right)$. Все дальнейшие сравнения - по модулю $q$.

$$\sum\limits_{x=0}^{q-1}\left(\frac{1-x^2}q\right) \equiv \sum\limits_{x=0}^{q-1}(1-x^2)^{\frac{q-1}2} = \sum\limits_{x=0}^{q-1} \sum\limits_{i=0}^{\frac{q-1}2} C_{\frac{q-1}2}^i (-x^2)^i = \sum\limits_{i=0}^{\frac{q-1}2} C_{\frac{q-1}2}^i (-1)^i \sum\limits_{x=0}^{q-1} x^{2i} = 1 + \sum\limits_{i=0}^{\frac{q-1}2} C_{\frac{q-1}2}^i (-1)^i \sum\limits_{x=1}^{q-1} x^{2i}$$

Теперь воспользуемся тем, что

$$\sum\limits_{x=1}^{q-1}x^j \equiv \begin{cases}-1, & q-1 | j \\ 0, & \mbox{ иначе }\end{cases}$$

. Ясно, что в последней сумме имеет смысл суммировать только при $i = 0$ и $i = \frac{q-1}2$.

$$N \equiv 1 - 1 - (-1)^{\frac{q-1}2} = -(-1)^{\frac{q-1}2} = -\left(\frac{-1}q\right)$$

,

что и требовалось доказать.