Нахождение значения предела

[MorozovBoris]

Добрый день! У Зорича приводятся два доказательства того, что $\lim\limits_{n\to\infty}\sqrt[n]n=1$ и $\lim\limits_{n\to\infty}\sqrt[n]a=1$ при любом $a>0$. Эти факты в изложении Зорича являются следствиями того, что $\lim\limits_{n\to\infty}\frac{n}{q^n}=0$ при $q>1$:
Следствие 1. $\lim\limits_{n\to\infty}\sqrt[n]n=1$.
При фиксированном $\varepsilon>0$ по доказанному найдётся $N\in\mathbb{N}$ такое, что при $n>N$ будем иметь $1\leqslant n<(1+\varepsilon)^n$. Тогда при $n>N$ получим $1\leqslant \sqrt[n]n<1+\varepsilon$ и, значит, действительно $\lim\limits_{n\to\infty}\sqrt[n]n=1$.
Следствие 2. $\lim\limits_{n\to\infty}\sqrt[n]a=1$.
Пусть $a\leqslant 1$. Для любого $\varepsilon>0$ найдем $N\in\mathbb{N}$ так, что при $n>N \ 1\leqslant a<(1+\varepsilon)^n$, и тогда при $n>N$ получаем $1\leqslant \sqrt[n]a<1+\varepsilon$, т.е. $\lim\limits_{n\to\infty}\sqrt[n]a=1$.
Если $0<a<1$, то $1<\frac{1}{a}$ и

$$\lim\limits_{n\to\infty}\sqrt[n]a=\lim\limits_{n\to\infty}\cfrac{1}{ \sqrt[n]{\cfrac{1}{a}\mathstrut}}=\cfrac{1}{ \lim\limits_{n\to\infty}\sqrt[n]{\cfrac{1}{a}\mathstrut}}=1.$$

В этих доказательствах мне неясно, каким образом находится n, удовлетворяющее данным неравенствам, и почему имеют силу эти неравенства.
Буду искренне благодарен за помощь!

[ewert]

MorozovBoris в сообщении #1411889 писал(а):

мне неясно, каким образом находится n, удовлетворяющее данным неравенствам,

Никак не находятся -- этого просто не нужно. Достаточно того, что известно об их существовании.

В первом следствии из того самого исходного предела следует, что $n<(1+\varepsilon)^n$, начиная с некоторого номера. Просто по определению предела -- поскольку отношение левой части неравенства к правой стремится к нулю. И абсолютно не важно, чему тот самый "некоторый номер" равен. Мы знаем, что он существует -- этого и достаточно.

Во втором следствии аналогично, но грубее. Из исходного неравенства следует, что геометрическая прогрессия стремится к бесконечности и, следовательно, рано или поздно больше любого $a\geqslant1$. Насколько рано или насколько поздно -- опять же не имеет значения.

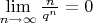
П.С. Зорич, однако же, здесь маленько нечестен. Подобные трюки (основанные на $\lim\limits_{n\to\infty}\frac{n}{q^n}=0$) принято проделывать до того, как становится известным, что такое корень энной степени и с какой стати он вообще существует.