Число помеченных графов

[classman]

Сколько разных помеченных графов можно получить путем перенумерации вершин полного двудольного графа $K_{n,n}$ с долями размера $n$.

-- 29.07.2019, 15:30 --

Ответ: $C^n_{2n}/2$
Натолкните на логику размышлений

[Connector]

Наверное, так: вершины, принадлежащие одной доле, неразличимы; сами доли неразличимы — граф, так сказать, симметричен.

[classman]

Connector в сообщении #1407669 писал(а):

Наверное, так: вершины, принадлежащие одной доле, неразличимы; сами доли неразличимы — граф, так сказать, симметричен.

Спасибо! Вроде понял.
$C^n_{2n}$ способов взять n вершин и поставить в одну из долей и нужно учесть, что доли неразличимы(т.е. n взятых вершин для первой доли предопределяют другие n вершин для второй), того $C^n_{2n}/2$ исходов.
Правильно мыслю?

[DeBill]

classman в сообщении #1407671 писал(а):

Правильно мыслю?

нет

[classman]

Объяснения не последуют?

[alcoholist]

classman
разбейте множество $C_{2n}^n$ помеченных графов на пары изоморфных

[DeBill]

classman в сообщении #1407671 писал(а):

$C^n_{2n}$ способов взять n вершин и поставить в одну из долей

И вершины, и доли у Вас уже заданы. Как это Вы их собираетесь "брать"?

classman в сообщении #1407671 писал(а):

доли неразличимы(

В каком смысле? И - что?

[classman]

DeBill в сообщении #1407770 писал(а):

И вершины, и доли у Вас уже заданы. Как это Вы их собираетесь "брать"?

Ну пускай будут не сами вершины, а их индексация.
"Доли не различимы", в том плане что, если поменять индексы первой доли со второй, новый граф не возникнет.
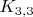
Если, например, у нас $K_{3,3}$, то индексации доли вида $1, 2, 3$ и $4, 5, 6$ эквивалентны.
Впрочем не важно, можно, конечно, докапываться до формулировки, но суть ясна

[DeBill]

classman
Да, так - хорошо.
Впрочем, и Ваша первое решение - тоже проходит, если сопроводить его нужными словами типа "изначально занымеруем все вершины, и будем генерировать двудольные графы"....