Ошибки Iго IIго рода

[jol]

Добрый день!

Правильно ли я понимаю, что в терминах условной вероятности, вероятность ошибок Iго и IIго рода соответственно:

$$\alpha = \Pr(H_1 \mid H_0), \qquad \beta = \Pr(H_0 \mid H_1)$$

[Lia]

Тема перемещена из форума «Математика (общие вопросы)» в форум «Помогите решить / разобраться (М)»

[--mS--]

Нет, неправильно понимаете. В обычной постановке $H_0$ и $H_1$ - не события, и у них нет вероятностей. А если бы они были событиями (взаимоисключающими), то обе выписанные Вами условные вероятности были бы равны нулю. В определении вероятностей ошибок критерия должен фигурировать критерий. И никаких условных вероятностей при этом не возникает, возникают вероятности при разных предположениях относительно распределения выборки:

$$ \alpha = \mathsf P(\text{критерий примет } H_1, \text{когда распределение выборки отвечает }H_0), $$ $$\beta = \mathsf P(\text{критерий примет } H_0, \text{когда распределение выборки отвечает }H_1), $$

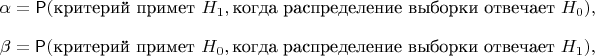
но это ни разу не условные вероятности. Точно такие же, как если бы Вам предложили найти $\mathsf P(X<2)$, сказав, что у $X$ стандартное нормальное распределение. А потом - что у $X$ распределение Пуассона с параметром $3$. Условными эти вероятности станут только в одном случае: если кто-то провёл случайный эксперимент, в результате которого с некоторыми вероятностями выбирается, из какого распределения быть выборке. Это называется "байесовская" постановка. При ней и только при ней слова "распределение выборки отвечает $H_0$" (то же, что "верна $H_0$") описывают событие, и определены условные вероятности "при условии, что верна $H_0$". То же для $H_1$.

[jol]

--mS--, спасибо :)