Столкнулся с необходимостью решить в общем уравнение:
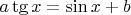
, где

Понятно, что это уравнение легко решить численно итерационными методами при заданных значениях

и

, но мне необходимо аналитическое решение в виде некоторой функции:

Что я пробовал: несложно, например, свести исходное уравнение к уравнению четвёртой степени путём замены

:
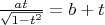
, откуда получается

Но решать это уравнение в общем виде по формулам Феррари тоже не вариант.
Ещё я раскладывал синус и косинус в ряды по степеням и искал обратный ряд. Но полученный ряд оказался не очень работоспособным из-за медленной сходимости.
Подскажите, в каком направлении можно ещё покопать. Меня устроит ответ, выраженный через любые специальные функции, или в виде сходящегося степенного ряда.
Можно ещё проанализировать граничные случаи для значений искомой функции:


Но как склеить эти асимптотики?..