Доброго времени суток. Поясните пожалуйста решение задачи (см.ниже).

Не понятны последние два абзаца (выделено красным):
1. почему каждому графу
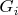
принадлежит
не более двух ребер наибольшего паросочетания?
Правильно я понимаю (см.рис.), что максимально, что можно "выжать" из графов
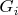
, это поменять местами паросочетания на концах увеличивающей цепи, если не нарушим паросочетания (на рис. показал стрелкой), и количество пар в этом случае может увеличиться в два раза?
2. в последнем абзаце опечатка? должно быть 12?